Уравнения и передаточные функции простейшей замкнутой импульсной системы.
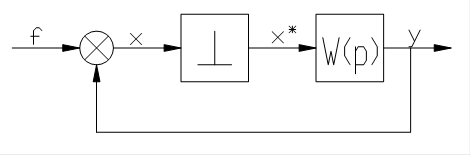 |
Рассмотрим замкнутую систему с импульсным элементом в цепи сигнала ошибки и единичной обратной связью. Структурная схема системы приведена на рис.10.
Рис.10
Запишем уравнение замыкания для дискретных моментов времени t=nT, n=0,1,...
x[n]=f[n]-y[n]. (26)
Для получения уравнения замкнутой системы воспользуемся уравнением разомкнутой системы
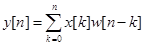 . (27)
. (27)
Подставив уравнение (26) в формулу (27), получим
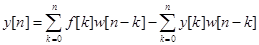 (28)
(28)
Для получения передаточной функции замкнутой импульсной системы применим Z -преобразование к обеим частям уравнения (28). С использованием теоремы свертки получим
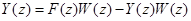 ,
,
откуда
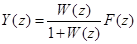 (29)
(29)
Выражение
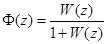
определяет передаточную функцию замкнутой импульсной системы для управляемой переменной по входному воздействию. Из уравнения (29) и уравнения замыкания в изображениях
X(z)=F(z)-Y(z)
получим для изображения ошибки
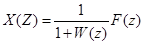 . (30)
. (30)
Выражение
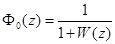
представляет собой передаточную функцию замкнутой системы по ошибке.
Пусть
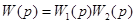
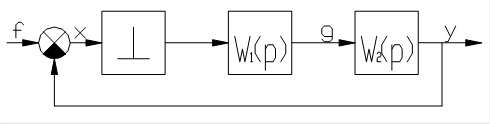
Найдем передаточную функцию замкнутой импульсной системы по отношению к сигналу g(t) на выходе звена с передаточной функцией 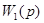 (рис.11). Выражение, связывающее переменные x(t) и g(t) в дискретные моменты времени имеет вид
(рис.11). Выражение, связывающее переменные x(t) и g(t) в дискретные моменты времени имеет вид
 |
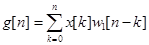
где 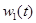 - весовая характеристика звена с передаточной функцией
- весовая характеристика звена с передаточной функцией 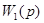 .
.
Рис.11
Применив Z-преобразование к обеим частям последнего уравнения, получим
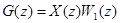 ,
,
где
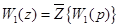
и, с учетом формулы (30), найдем
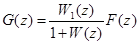 .
.
Таким образом, искомая передаточная функция имеет вид
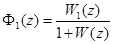
Пример. Найти передаточные функции замкнутой системы 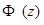 и
и 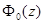 . Приведенная непрерывная часть системы та же, что и в примере предыдущей лекции.
. Приведенная непрерывная часть системы та же, что и в примере предыдущей лекции.
В результате решения предыдущего примера было найдено
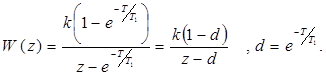
Тогда
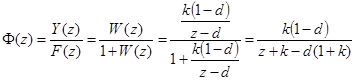 ;
;
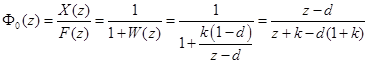 .
.
Дата добавления: 2016-07-05; просмотров: 2648;











