ВИЗНАЧЕННЯ ПРИСКОРЕНЬ ГРУПИ 2 КЛАСУ ПЕРШОГО ВИДУ
ВИЗНАЧЕННЯ ШВИДКОСТЕЙ І ПРИСКОРЕНЬ СТРУКТУРНИХ ГРУП II КЛАСУ МЕТОДОМ ПЛАНІВ
Розглянемо структурну групу Ассура 2 класу 2 порядку 1 виду. Попередньо в масштабі зображуємо структурну групу (рис. 1, а), що включає ланки 2,3, які утворюють обертальну кінематичну пару (КП) 5 класу. Зовнішніми КП В, D група може приєднуватися до інших ланок.
 |
Задано 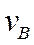 ,
, 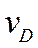 .
.
Визначити 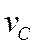 ,
, 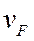 ,
, 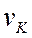 ,
, 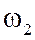 ,
, 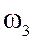 .
.
Використаємо теорему про додавання швидкостей, яка за складного руху точки стверджує:
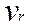
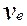 АБСОЛЮТНА ШВИДКІСТЬ
АБСОЛЮТНА ШВИДКІСТЬ 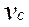 ТОЧКИ C ДОРІВНЮЄ ГЕОМЕТРИЧНІЙ СУМІ ПЕРЕНОСНОЇ ТА ВІДНОСНОЇ ШВИДКОСТІ ЦІЄЇ ТОЧКИ.
ТОЧКИ C ДОРІВНЮЄ ГЕОМЕТРИЧНІЙ СУМІ ПЕРЕНОСНОЇ ТА ВІДНОСНОЇ ШВИДКОСТІ ЦІЄЇ ТОЧКИ.
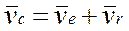 (1)
(1)
При плоскому русі ланки переносний рух є поступальним зі швидкістю довільно обраної точки ланки, прийнятої за полюс, а відносний рух є обертальним навколо цієї точки.
Співвідношення (1) використовують для побудови планів швидкостей і прискорень точок.
Таким чином, рух точки C групи може бути розкладеним на переносно-поступальний зі швидкістю точки B (чи точки D) і відносно-обертальний навколо точки B чи точки D відповідно.
Тоді система векторних рівнянь для швидкості точки C має вигляд:
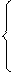


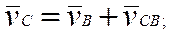 (3)
(3)
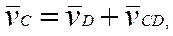 (4)
(4)
де, 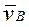 ,
, 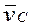 ,
, 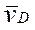 , - вектори абсолютних швидкостей точок B,C,D,
, - вектори абсолютних швидкостей точок B,C,D,
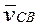 ,
, 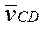 , - вектори відносних швидкостей точки C відносно точок B и D.
, - вектори відносних швидкостей точки C відносно точок B и D.
Приймаємо як полюс плану швидкостей точку Р, з якої в довільно обраному масштабі 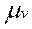 =
= 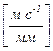 проводимо вектори (рb) і (рd) заданих абсолютних швидкостей точок B і D (рис. 1, б).
проводимо вектори (рb) і (рd) заданих абсолютних швидкостей точок B і D (рис. 1, б).
Довжини векторів (рb) і (рd) визначаємо за формулами:
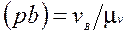 (5)
(5)
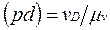 (6)
(6)
Вектори відносних швидкостей будуть спрямовані перпендикулярно відповідно до ланок ВР, СD. Тому з точки (b) проводимо пряму перпендикулярну ланці BC, із точки (d) - пряму перпендикулярну ланці CD.
Точку перетину цих прямих позначимо C і з'єднаємо її з полюсом Р. Вектор (pc) у масштабі буде представляти шукану абсолютну швидкість точки C.
Величину швидкості точки C визначаємо за формулою:
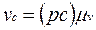 (7)
(7)
де (рс) - довжина відрізка (рв) на плані швидкостей, мм.
Відрізки (cb) і (cd) являють собою вектори відносних швидкостей, відповідно точки C відносно B і точки C відносно D.
Отже,
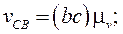 (8)
(8)
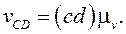 (9)
(9)
Трикутник рbс і трикутник рсd називають планами швидкостей ланок 1 і 3, а фігура рbсd - планом швидкостей групи BCD.
Точка р - полюс плану швидкостей.
2. ВИЗНАЧЕННЯ КУТОВИХ ШВИДКОСТЕЙ З ПОБУДОВАНОГО ПЛАНУ
Для визначення кутової швидкості якої-небудь ланки необхідно значення відносної швидкості яких-небудь точок ланки поділити на відстань між цими точками. Використовуючи наведене правило, визначимо кутову швидкість ланок 1, 2.
З урахуванням (8), (9) маємо:

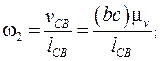 (10)
(10)
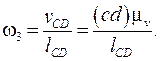 (11)
(11)
НАПРЯМОК кутових швидкостей ланок визначаємо переносом відносної швидкості точки, наприклад, C відносно B у досліджувану точку C схеми групи і т.д.
На підставі цього, для визначення напрямку кутової швидкості ланки 1 вектор відносної швидкості переносимо в точку C групи і розглядаємо напрямок її руху відносно точки B (за годинниковій стрілці).
Аналогічно виконуємо перенесення вектора відносної швидкості у точку C групи. Для ланки 2 маємо напрямок кутової швидкості - проти годинникової стрілки. Зазначені напрямки відзначаємо на ланках досліджуваної групи.
3. ВИЗНАЧЕННЯ ШВИДКОСТІ ЯКОЇ-НЕБУДЬ ТОЧКИ, ЩО ЗНАХОДИТЬСЯ НА ОСІ ЛАНКИ
Для визначення швидкості якої-небудь точки К, що лежить на осі
ланки ВР складемо векторне рівняння:
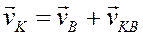 (12)
(12)
Величина відрізка (вк), що зображує швидкість точки К відносно В визначимо з наступних залежностей:

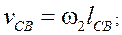 (13)
(13)

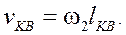 (14)
(14)
Розділимо почленно 14 на 13:
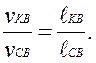 (15)
(15)
З формули (15) випливає, що швидкості точок К і С відносно точки В прямо пропорційні відстаням цих точок до точки В. Підставляючи замість швидкостей відповідні відрізки з плану швидкостей, маємо:
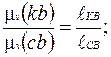 (16)
(16)
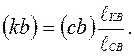 (17)
(17)
З (17) випливає, що для визначення (кb) необхідно відрізок (вс) розділити в тім же відношенні в якому точка В поділяє ланку на схемі групи.
З'єднуючи точку (к) з полюсом (р) маємо відрізок (рк), який у масштабі являє собою абсолютну швидкість точки К.
4. ВИЗНАЧЕННЯ ШВИДКОСТІ ДОВІЛЬНОЇ ТОЧКИ ЛАНКИ
Для визначення швидкості довільної точки F ланки 1 складемо наступні векторні рівняння:
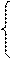
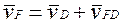 (18)
(18)
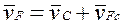 (19)
(19)
Вектори абсолютних швидкостей точок C і D відомі за величиною і напрямком, а вектори відносних швидкостей відомі лише за напрямком.
Отже, з т. С плану швидкостей проведемо пряму перпендикулярну (FC), а через точку (d) - пряму перпендикулярну до (CD). Точка перетину (f) і визначить закінчення вектора (pf).
Маємо:
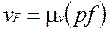 (20)
(20)
Розглядаючи трикутник cdf плану швидкостей і CDF на ланці неважко побачити їх подібність, тому що сторони взаємно перпендикулярні.
Ця ВЛАСТИВІСТЬ ПОДІБНОСТІ фігури відносних швидкостей і фігури ланки на схемі механізму дозволяє визначити швидкості будь-яких точок цієї ланки не з рівнянь, а графічно побудовою подібних фігур.
Побудовані подібні фігури повинні бути СХОЖЕ РОЗТАШОВАНІ, тобто мусить збігатися порядок букв на схемі і плані швидкостей.
Для прикладу, розглянемо кривошипно-коромисловий механізм (шарнірний чотириланковик).
ВИЗНАЧЕННЯ ПРИСКОРЕНЬ ГРУПИ 2 КЛАСУ ПЕРШОГО ВИДУ
5.1. ВИЗНАЧЕННЯ ЛІНІЙНИХ ПРИСКОРЕНЬ ТОЧОК ЛАНОК.
Для розв’язання поставленої задачі необхідно знати вектори абсолютних прискорень точок B і D (рис. 2,а). Крім того план швидкостей передбачається побудованим (рис. 1,б) і, отже, відомі швидкості всіх ланок групи.
АБСОЛЮТНЕ ПРИСКОРЕННЯ будь-якої точки ланки за плоскопаралельного (плоского) руху твердого тіла дорівнює ГЕОМЕТРИЧНІЙ СУМІ двох прискорень: прискорення в поступальному ПЕРЕНОСНОМУ русі і прискорення в обертальному ВІДНОСНОМУ русі:
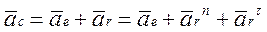 (2)
(2)
де 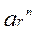 - НОРМАЛЬНЕ ПРИСКОРЕННЯ у відносному русі, спрямоване по радіусу обертання точки до ЦЕНТРА КРИВИЗНИ траєкторії;
- НОРМАЛЬНЕ ПРИСКОРЕННЯ у відносному русі, спрямоване по радіусу обертання точки до ЦЕНТРА КРИВИЗНИ траєкторії;
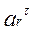 - тангенціальне (КОЛОВЕ) прискорення, спрямоване ПЕРПЕНДИКУЛЯРНО радіусу обертання.
- тангенціальне (КОЛОВЕ) прискорення, спрямоване ПЕРПЕНДИКУЛЯРНО радіусу обертання.
Для визначення прискорення т. C розглядаємо її рух як складний, що складається з переносного поступального зі швидкостями і прискореннями точок B і D і відносного обертального навколо цих точок. Тоді векторні рівняння для визначення прискорення точки C:
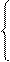
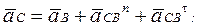 (21)
(21)
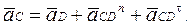 (22)
(22)
де 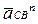 ,
, 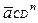 - нормальні прискорення у відносному русі;
- нормальні прискорення у відносному русі;
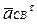 ,
, 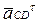 - тангенціальні прискорення у відносному русі.
- тангенціальні прискорення у відносному русі.
Вектори нормальних прискорень у відносному русі можуть бути
визначені так:
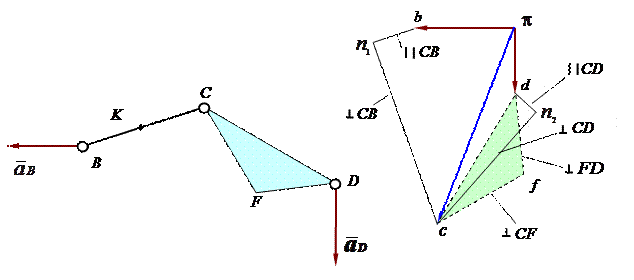
 а) б)
а) б)
Рис.2.
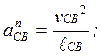 (23)
(23)
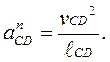 (24)
(24)
Лінійні і кутові швидкості можуть бути визначені за побудованим планом швидкостей, довжини ланок визначаються з кінематичної схеми.
Підставляючи в отримані рівності значення швидкостей та довжини ланок, маємо
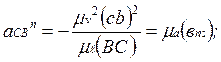 (25)
(25)
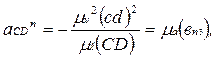 (26)
(26)
де відрізки (bc) і (dc) повинні бути узяті з плану швидкостей.
Вектор нормального прискорення 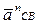 спрямований від точки C до точки B паралельно напрямку CВ, а вектор нормального прискорення
спрямований від точки C до точки B паралельно напрямку CВ, а вектор нормального прискорення 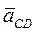 спрямований від точки C до точки D паралельно напрямку CD.
спрямований від точки C до точки D паралельно напрямку CD.
Після цього, у рівняннях (21), (22) невідомими залишаються лише величини векторів тангенціальних прискорень, які можуть бути визначені наступною графічною побудовою.
Вибираємо як полюс плану прискорень точку 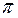 (рис. 2,б) і відкладаємо відрізки (па) і (пb), що являють у масштабі прискорення точок В и D. Далі, зкориставшись рівняннями (23), (24), обчислюємо величини нормальних прискорень і відкладаємо з точок b і d відрізки (bn1) і (bn2), що представляють у масштабі ці прискорення.
(рис. 2,б) і відкладаємо відрізки (па) і (пb), що являють у масштабі прискорення точок В и D. Далі, зкориставшись рівняннями (23), (24), обчислюємо величини нормальних прискорень і відкладаємо з точок b і d відрізки (bn1) і (bn2), що представляють у масштабі ці прискорення.
З отриманих точок n1 і n2 проводимо прямі в напрямках векторів тангенціальних прискорень перпендикулярно до напрямків BC і CD. Точка перетинання цих прямих і дасть закінчення вектора повного прискорення точки C.
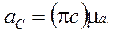 (27)
(27)
З'єднавши точки b і d плану з точкою с, одержимо вектори повних відносних прискорень точок В і D відносно точки С.
Маємо
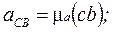
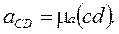 (28)
(28)
5.2. ВИЗНАЧЕННЯ КУТОВИХ ПРИСКОРЕНЬ ЛАНОК.
Модулі кутових прискорень ланок BC і CD будуть рівні
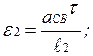
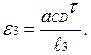 (29)
(29)
Підставляючи в рівність (29) відповідні відрізки, узяті з плану прискорень і зі схеми, маємо
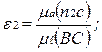

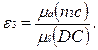 (30)
(30)
Напрямки кутових прискорень можуть бути визначені так: переносимо подумки вектори тангенціальних складових прискорень у точку C та розглядаємо їх відносно точок В та D.
5.3. ВИЗНАЧЕННЯ ПРИСКОРЕННЯ ДОВІЛЬНОЇ ТОЧКИ ЛАНКИ.
Для визначення прискорення довільної точки F жорстко зв'язаний з ланкою 2 (рис.2, а) можна також графічно вирішити систему векторних рівнянь для шуканої точки F відносно точок C і D, прискорення яких відомі. Рівняння складаються аналогічно (21), (22).
Для вирішення цієї задачі можна також скористатися вищенаведеним правилом подібності. Для цього будуємо на відрізку (cd) плану прискорень трикутник cdf, подібний і схоже розташований до трикутника CDF на схемі.
Враховуючи, що всі сторони трикутника cdf повернені відносно трикутника CDF на постійний кут, то побудова подібного трикутника на плані прискорень зручно вести, заміряючи кути між сусідніми сторонами DC, DF, і CD, CF. При обході контуру cdf у якому-небудь напрямку порядок букв мусить збігатися з порядком букв контуру CDF.
Подібно тому як це мало місце в задачі про швидкості, вектори повних прискорень усіх точок ланок мають своїм початком точку 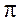 - полюс плану прискорень, а вектори усіх відносних прискорень з'єднують собою кінці векторів повних прискорень.
- полюс плану прискорень, а вектори усіх відносних прискорень з'єднують собою кінці векторів повних прискорень.
Самостійно визначити лінійні, кутові швидкості і прискорення ланок кривошипно-коромислового механізму (рис.3).
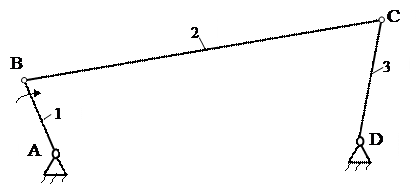 |
Рис.3.
Вихідними даними є: кутова швидкість ланки 1 (кривошип); Приймаємо 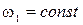 ; відомі також лінійні розміри всіх ланок l1, l2, l3, l4.
; відомі також лінійні розміри всіх ланок l1, l2, l3, l4.
| <== предыдущая лекция | | | следующая лекция ==> |
| ВИЗНАЧЕННЯ ПОЛОЖЕНЬ ЛАНОК ГРУП І ПОБУДОВА ТРАЄКТОРІЙ, ОПИСУВАНИХ ТОЧКАМИ ЛАНОК МЕХАНІЗМУ. | | | АНАЛОГИ ШВИДКОСТЕЙ І ПРИСКОРЕНЬ |
Дата добавления: 2016-06-15; просмотров: 2310;











