Расчет трехфазных цепей

Соединение в звезду

Алгоритм решения задач

1. Обозначить на схеме все токи и напряжения.

2. Определить фазные напряжения генератора.

3. Определить комплексные фазные сопротивления потребителя энергии.

4. Определить напряжение смещения нейтрали.

Если нагрузка симметричная (Z_a = Z_b = Z_c ) или есть нейтральный провод, сопротивление которого равно нулю, то = 0.

5. Определить фазные напряжения потребителя энергии.

= - ;

= - ;

= - .

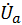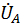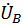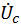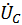6. Определить линейные токи.

= ; = / ; = / .

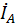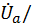
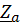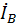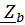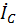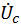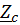7. Определить ток в нейтрале.

= + + .

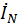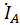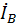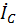8. Проверить результат по уравнению баланса мощностей.

∑ S_ист= ∑ S_потр;

∑ S_ист= S_A+S_B+S_C= ^*+ ^*+ ^*;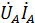

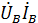∑ S_потр= P + jQ.

P = R_aI_A² + R_bI_B² + R_cI_C²

Q =± X_aI_A² ± X_bI_B² ± X_СI_C²

(+) – для индуктивного сопротивления X_L

(--) – для емкостного сопротивления X_C

S =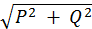

9. Построить векторную диаграмму токов и напряжений.

Задача.

Определить токи, мощности и построить векторную диаграмму токов и напряжений.

1. Обозначаем на схеме все токи и напряжения.

2. Определяем фазные напряжения генератора.

U_ф =U_л / 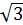= 380 / 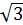= 220 B.

= 220 B; = 220 e ^–j120º B; = 220 e^j120º B.

Представим эти напряжения в алгебраической форме записи.

= 220 B;

= (220 cos120º - j220 sin120º ) = -110 – j190 B;

= ( 220 cos120º + j220 sin120º ) = -110 + j190 B.

3. Определяем фазные сопротивления потребителя энергии.

Z_a = R + jX_L= 4 + j3 Ом; Z_a = 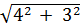e^j37º = 5 e^j37º Ом;

Z_b= R - jX_C= 4 - j3 Ом; Z_b= 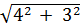e^-j37º = 5 e ^-j37º Ом;

Z_c= jX_L= j3 = 3 e^j90º Ом.

4. Определяем напряжение смещения нейтрали.

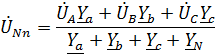
Комплексные фазные проводимости

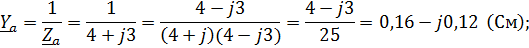
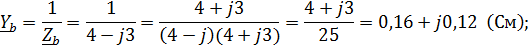
Y_N=О

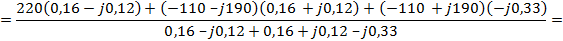
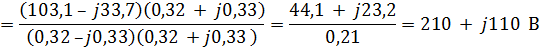
Представим напряжение смещения нейтрали в показательной форме записи.

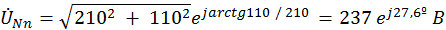
5. Определим фазные напряжения потребителя энергии.

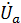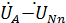= = 220 – 210 – j110 = 10 – j110 B;

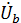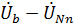= = -110 – j190 – 210 – j110 = - 320 – j300 B;

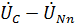= = -110 + j190 – 210 – j110 = - 320 + j80 B.

Действующие значения этих напряжений.

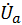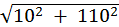= = 110,5 B;

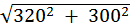= = 438,6 B;

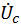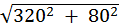= = 330 B.

Так как нагрузка несимметричная и отсутствует нейтральный провод, фазные напряжения – разные.

6. Определим линейные токи.

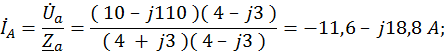
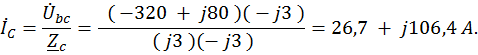
Действующие значения этих токов.

I_A= 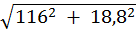= 22 A;

I_B= = 87,7 A;

I_C = 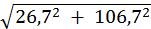= 110 A

7. Проверяем наличие тока в нейтрале.

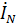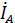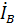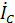= + + = -11,6 – j18,8 – 15,2 – j86,4 + 26,7 + j106,4 = 0

8. Проверим результат по уравнению баланса мощностей.

∑ S_ист= S_A+S_B+S_C= 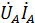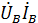^*+ ^*+ ^* =220 ( -11,6 + j18,8 ) +

+ ( -110 – j190 )( -15,2 + j86,4 ) + ( -119 + j190 )( 26,7 – j106,7 ) =

= 32,8 + j14,3 кВА;

P_потр =R_aI_A² + R_bI_B² = 4٠22² + 4٠87,7² = 32,7 кВт;

Q_потр = + X_LI_A² - XcI_B² + X_LI_C² = 3٠22² - 3٠87,7² + 3٠110² = 14,6 кВАр;

S_потр = 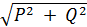= 35,8 кВА;

∑ S_потр= P + jQ = 32,7 + j14,6 кВА;

∑ S_ист= ∑ S_потр

С учетом погрешности округления цифр результаты расчета правильны.

9. Строим векторную диаграмму токов и напряжений.

Задача.

Определить токи, мощности и построить векторную диаграмму токов и напряжений. В данной схеме есть нейтральный провод, поэтому каждую фазу можно рассчитывать как однофазную цепь.

1. Обозначим на схеме все токи и напряжения.

2. Определяем фазные напряжения генератора.

U_ф =U_л / 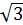= 380 / 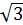= 220 B

= 220 B; = 220 e ^–j120º B; = 220 e^j120º B

Представим их в алгебраической форме записи.

= 220 B;

= ( 220 cos120º - j220 sin120º ) = -110 – j190 B;

= ( 220 cos120º + j220 sin120º ) = -110 + j190 B

3. Определим полные сопротивления фаз и углы сдвига фаз между фазными токами и фазными напряжениями.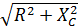

Z_a= 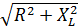= 5Ом; φ'_a= arctg(X_L / R) = 37º

Z_b= 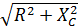= 5 Ом; φ'_b= - arctg(X_C / R) = - 37º

Z_c = X_L = 3 Ом; φ'_c= 90º

4. Сопротивление нейтрального провода равно нулю U_Nn = 0. На векторной диаграмме точки n и N совпадут. В этом случае фазные напряжения потребителя энергии равны фазным напряжениям генератора. Получаем симметричную систему фазных напряжений потребителя.

U_a = U_b =U_c = U_ф = 220 В

5. Определим действующие значения линейных токов.

I_A = U_ф / Z_a = 220 / 5 = 44 A;

I_B = U_ф / Z_b = 220 / 5 = 44 A;

I_C = U_ф / Z_c = 220 / 3 = 73A

6. Ток в нейтральном проводе можно определить из векторной диаграммы, сложив векторы линейных токов.

= + +

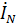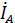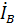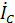
Его можно определить и численно, но в этом случае необходимо углы сдвига фаз привести к началу координат.

φ_a= 0 - φ'_a= 0 -37º = - 37º;

φ_b= -120º - φ'_b= -120º - ( -37º ) = -83º;

φ_c=120º - φ'_c= 120º - 90º = 30º

Линейные токи и ток в нейтральном проводе можно представить в комплексной форме.

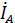= I_A e^{–j37 º}= 44 e ^{–j37 º}= 44cos37º - j44 sin37º = 35,14- j26,5 A;

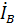= I_B e^{–j83 º} = 44 e ^{–j83 º}= 44 cos83º - j44 sin 83º = 5,4 – j43,7 A;

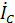= I_C e^{j30 º} = 73 e ^{j30 º}= 73cos 30º + j73 sin 30º = 63,2+ j36,5 A;

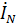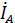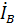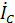= + + = 103,74 – j33,7 =109 e ^{–j18 º}A

7. Проверяем результат по уравнению баланса мощностей.

∑ S_ист= S_A+S_B+S_C= 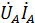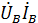^*+ ^*+ ^* = 220 ( 35,14 – j26,5 ) +

+ ( -110 – j190 )( 5,4 – j43,7) + ( -119 + j190 )( 63,2 + j36,5) =

= 15,2 + j16 кВА;

P_потр =R_aI_A² + R_bI_B² = 4٠44² + 4٠44 = 15,5 кВт;

Q_потр = + X_LI_A² - X_CI_B² + X_LI_C² = 3٠44² - 3٠44² + 3٠73² = 16 квар;

S_потр = 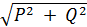= 22,3кВА;

∑ S_потр= P + jQ = 15,5 + j16 кВА ;

∑ S_ист= ∑ S_потр

С учетом погрешности округления цифр результаты расчета правильны.

8. Строим векторную диаграмму токов и напряжений.

Задача.

Определить токи, мощности и построить векторную диаграмму токов и напряжений.

1. Определяем фазное напряжение.

U_ф=U_л / 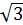= 220 / 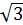= 127 B.

2 . Определяем комплексные сопротивления фаз.

Z_ф = Z_a = Z_b = Z_c= R - jX_C.

Комплексные сопротивления фаз равны, следовательно, нагрузка симметричная,

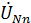= 0 и 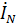= 0. Нейтральный провод в данной схеме не нужен.

3. Определяем полные сопротивления фаз и углы сдвига фаз между линейными токами и фазными напряжениями.

Z_ф= 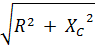= 5 Ом; φ= - arctg(Xc / R) = - 53º

4. Определяем действующие значения линейных токов.

I_л = I_ф=U_ф / Z_ф = 127 / 5 = 25,4 A.

5. Определяем активную, реактивную и полную мощности.

P = 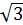U_лI_лcosφ = 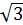220٠25,4cos 53º =5,82 кВт;

Q = 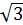U_лI_лsinφ = 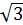220٠25,4 sin 53º =7,72 квар;

S = 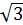U_лI_л = 9.667 кВA.

6. Построение векторной диаграммы токов и напряжений.