Метод суперпозиции.

Метод основан на принципе суперпозиции. Ток и напряжение каждой ветви цепи равен сумме (с учетом знака) токов и соответственно напряжений, создаваемых каждым из источников. Метод применим только для линейных цепей.

Алгоритм решения задач методом суперпозиции.

1. Разделить исходную схему на отдельные частные схемы, в каждой из которых только один источник. Остальные источники заменить их внутренними сопротивлениями.

2. Определить токи в ветвях частных схем.

3. Определить токи в ветвях исходной схемы, как сумму (с учетом знака) токов в тех же ветвях.

4. Проверить результат по уравнению баланса мощностей

Задача.

Определить токи в ветвях методом наложения.

1. Разделим исходную схему на отдельные частные схемы.

2. Определим токи в ветвях частных схем.

R₂₃ = 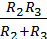=2 Ом; I₁' = = 10 A ; U'_ab =R₂₃I₁' = 20 B ;

I₂' = U'_ab/ R₂=5 A; I₃' = U'_ab/ R₃ =5 A.

R₁₃ = 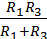= 2,4 Ом; I₂'' = 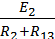= 10 A; U''_ab = R₁₃ I₂'' = 24 B ;

I₁'' = U''_ab/ R₁= 4 A; I₃'' = U''_ab/ R₃ = 6 A.

3. Определим токи в ветвях исходной схемы.

I₁ = I₁' + I₁'' = 14 А; I₂ =I₂' + I₂'' = 15 А; I₃ =I₃'' - I₃' = 1 А.

4. Проверка результата по уравнению баланса мощностей

Оба источника работают в режиме генерирования.

ΣP_ист =Σ P_потр

E₁ I₁ + E₂ I₂ = R₁ I₁² + R₂ I₂² + R₃ I₃²

2080 = 2080

Получили тождество, следовательно, решение верно.