Найпростіші задачі аналітичної геометрії
1. Відстань між двома точками.
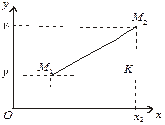 Рис. 3.4
Рис. 3.4
|
Нехай задано дві точки М1 (х1, у1) і
М2 (х2, у2) (рис. 2.10).
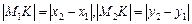 .
.
Трикутник М1М2K — прямокутний, тому за теоремою Піфагора маємо:
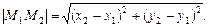 (3.7)
(3.7)
2. Поділ відрізка у заданому відношенні.
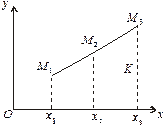 Рис. 3.5
Рис. 3.5
|
Число l — називається відношенням, в якому точка М ділить відрізок М1М2 (рис. 2.11), якщо
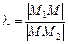 .
.
Нехай задано l і координати точок 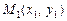 і
і 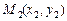 , треба знайти координати точки М (х, у).
, треба знайти координати точки М (х, у).
З рис. 2.11 і теореми про пропорційні відрізки, що відтинають паралельні прямі на сторонах кута, випливають співвідношення:
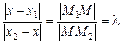 .
.
Оскільки числа х – х1 і х2 – х одного й того самого знака (при х1 < х2 вони додатні, а при х1 > х2 — від’ємні), то 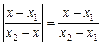 . Отже,
. Отже, 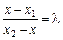 .
.
Звідси:
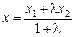 . (3.5)
. (3.5)
Аналогічно до попереднього дістанемо формулу для знаходження координати у
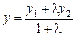 . (3.6)
. (3.6)
Наслідок. Якщо точка М (х, у) — середина відрізка М1 М2, то
l = 1 і формули (2.11), (2.12) набирають вигляду:
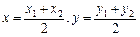 .
.
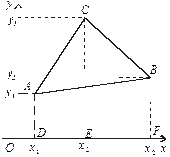 Рис. 2.12
Рис. 2.12
|
3. Площа трикутника.
Нехай задано координати вершин деякого трикутника А (х1, у1), В (х2, у2), С (х3, у3) (рис. 2.12).
Знайдемо площу цього трикутника.
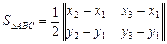
Тема 4. Пряма на площині і в просторі
План
1. Рівняння прямої у просторі.
2. Взаємне розміщення прямої і площини у просторі.
Рівняння прямої у просторі
Пряму у просторі можна задати як лінію перетину двох площин у прямокутній системі координат:
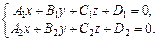 (4.1)
(4.1)
Зрозуміло, що ці площини мають бути непаралельними, тобто їхні нормальні вектори 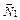 ,
, 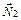 — не колінеарні. Система (2.31) називається загальним рівнянням прямої. Дістанемо ще деякі форми рівняння прямої.
— не колінеарні. Система (2.31) називається загальним рівнянням прямої. Дістанемо ще деякі форми рівняння прямої.
Канонічне рівняння прямої. Нехай у системі координат Охуz задано пряму l і ненульовий вектор 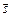 , колінеарний цій прямій. Точка
, колінеарний цій прямій. Точка 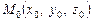 належить прямій, а напрямний вектор
належить прямій, а напрямний вектор 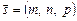 . Тоді довільна точка М (х, у, z) лежатиме на прямій тоді і тільки тоді, коли вектори
. Тоді довільна точка М (х, у, z) лежатиме на прямій тоді і тільки тоді, коли вектори 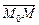 і
і 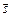 колінеарні:
колінеарні:
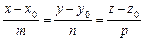 . (4.2)
. (4.2)
Рівняння (2.32) називається канонічним рівнянням прямої у просторі.
Параметричне рівняння.
У рівнянні прямої (2.32) позначимо через t кожне з рівних відношень. Тоді
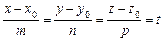 .
.
Звідси дістаємо:
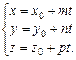
Параметричне рівняння прямої в просторі.
Рівняння прямої, що проходить через дві задані точки.
Нехай дві точки 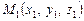 і
і 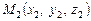 належать прямій у просторі. Тоді вектор
належать прямій у просторі. Тоді вектор 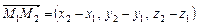 можна розглядати як напрямний вектор прямої. Замінюючи ним вектор
можна розглядати як напрямний вектор прямої. Замінюючи ним вектор 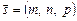 у рівнянні (2.32), дістанемо шукане рівняння прямої у просторі
у рівнянні (2.32), дістанемо шукане рівняння прямої у просторі
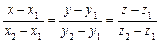 .
.
Для знаходження кута між двома прямими
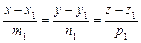 і
і 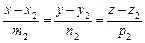
візьмемо до уваги, що вектори 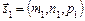 і
і 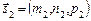 колінеарні відповідним прямим і скористаємося формулою:
колінеарні відповідним прямим і скористаємося формулою:
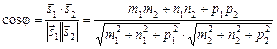 .
.
З останньої формули випливає умова перпендикулярності двох прямих
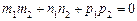 ,
,
а умову паралельності двох прямих дістанемо як умову колінеарності напрямних векторів 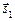 і
і 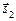 :
:
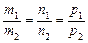 .
.
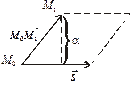
|
Розглянемо ще задачу знаходження відстані від точки 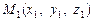 до прямої
до прямої 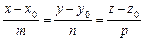 .
.
| Рис. 4.1 |
Шукану відстань можна розглянути як довжину висоти паралелограма, побудованого на векторах 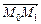 і
і 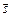 (рис. 4.1). Відомо, що площа паралелограма дорівнює модулю векторного добутку векторів, на яких побудовано цей паралелограм. Доходимо висновку, що шукану висоту, а отже, і відстань від точки до прямої можна знайти за формулою:
(рис. 4.1). Відомо, що площа паралелограма дорівнює модулю векторного добутку векторів, на яких побудовано цей паралелограм. Доходимо висновку, що шукану висоту, а отже, і відстань від точки до прямої можна знайти за формулою:
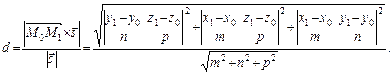 (4.3)
(4.3)
Дата добавления: 2016-05-26; просмотров: 3600;











