Взаємне розміщення прямої і площини у просторі
Нехай задано пряму 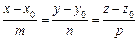 і площину
і площину 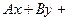
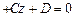 у просторі. Якщо
у просторі. Якщо
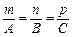 ,
,
то пряма перпендикулярна до площини, а коли
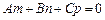 ,
,
пряма паралельна площині.
Нехай 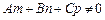 . Знайдемо координати точки перетину площини і прямої. Перейдемо до канонічного рівняння прямої
. Знайдемо координати точки перетину площини і прямої. Перейдемо до канонічного рівняння прямої
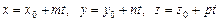
Знайдемо кут між площиною і прямою.
| Рис. 4.2 |
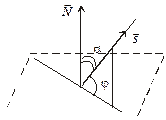
Кут j між площиною і прямою дорівнює куту між прямою і її проекцією на площину (рис. 2.24). Вектор 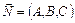 — перпендикулярний до площини, а кут a, який він утворює з вектором
— перпендикулярний до площини, а кут a, який він утворює з вектором 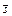 , разом з j у сумі дорівнює 90°. Тобто a + j = 90°.
, разом з j у сумі дорівнює 90°. Тобто a + j = 90°.
Знайдемо кут a як кут між двома векторами.
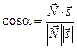 .
.
Якщо 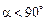 , то
, то 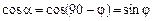 , а якщо
, а якщо 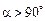 , то
, то 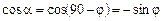 , у будь-якому разі
, у будь-якому разі 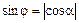 . Отже,
. Отже,
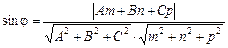 .
.
Тема 5. Криві другого порядку
План
1. Канонічне рівняння еліпса.
2. Канонічне рівнянням гіперболи.
3. Канонічне рівнянням параболи і кола.
Розглянемо тепер лінії другого порядку, які на площині в загальному випадку можна записати так:
а11х2 + 2а12ху + а22у2 + 2а13х + 2а23у + а33 = 0. (5.1)
Рівняння (2.19) описує всі криві другого порядку в загальному випадку. Спинимось спочатку на простіших, так званих канонічних рівняннях ліній другого порядку.
Еліпс.Означення. Множина точок площини, для яких сума відстаней від двох заданих точок, що називаються фокусами, є величина стала й така, що дорівнює 2а і більша, ніж відстань між фокусами, називається еліпсом.
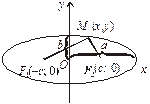 Рис. 5.1
Рис. 5.1
|
На рис. 2.16 зображено F1 (–c, 0),
F2 (c, 0) — фокуси еліпса, М (х, у) — точка множини, яка задовольняє означення, тобто 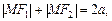 причому 2с < < 2a Þ a > c.
причому 2с < < 2a Þ a > c.
Тоді
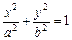 (5.2)
(5.2)
канонічне рівняння еліпса, де b2 = а2 – с2.
Розглянемо геометричний зміст параметрів, що входять в рівняння (5.2). Якщо х = 0, у = ± b, тобто точки (0, b) і (0, – b) є точками перетину еліпса з віссю Оy. Відрізок завдовжки b називають малою піввіссю еліпса. При у=0, х=±а і відповідно (а,0); (– а; 0) є точками перетину еліпса з віссю Ох. Відрізок завдовжки а — велика піввісь еліпса. З парності виразу (5.2) за х і за у випливає симетрія еліпса відносно осей Ох і Оу. На рис. 5.1 зображено еліпс.
Ексцентриситет еліпса — це відношення 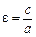 ; за означенням с <a і eÎ[0, 1). Оскільки
; за означенням с <a і eÎ[0, 1). Оскільки 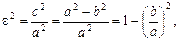 то
то 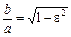 . З останньої рівності випливає геометричний зміст ексцентриситету, який полягає в тому, що він характеризує ступінь витягнутості еліпса. Так, при
. З останньої рівності випливає геометричний зміст ексцентриситету, який полягає в тому, що він характеризує ступінь витягнутості еліпса. Так, при 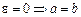 маємо коло, якщо e наближається до одиниці, то відношення довжини півосей еліпса стає малим, тобто еліпс витягується вздовж осі Ох.
маємо коло, якщо e наближається до одиниці, то відношення довжини півосей еліпса стає малим, тобто еліпс витягується вздовж осі Ох.
Гіпербола.Означення. Множина точок площини, для яких модуль різниці відстаней від двох заданих точок, що називаються фокусами, є величиною сталою, яка дорівнює 2а і менша за відстань між фокусами, називається гіперболою.
Скористаємось рис. 2.17, з якого бачимо, що точки F1 (– c, 0) і F2 (c, 0) — фокуси гіперболи, точка М (х, у) — точка визначеної множини. Тоді 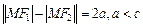 .
.
Канонічне рівняння гіперболи має вигляд:
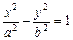 , де b2 = c2 – a2.
, де b2 = c2 – a2.
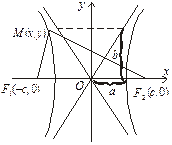 Рис. 5.2
Рис. 5.2
|
Дослідимо здобуте рівняння. Гіпербола не перетинає вісь Оу. При у = 0;
х=±а і точки (–а,0); (а,0) — точки перетину з віссю Ох. Розглянемо ще рівняння прямих 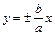 , які далі називатимемо асимптотами гіперболи. Враховуючи симетрію відносно осей Ох і Оу, будуємо графік гіперболи, який зображено на рис. 5.2.
, які далі називатимемо асимптотами гіперболи. Враховуючи симетрію відносно осей Ох і Оу, будуємо графік гіперболи, який зображено на рис. 5.2.
Відрізки завдовжки b і а називають відповідно уявною і дійсною осями гіперболи.
Ексцентриситет гіперболи 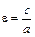 , але с > a і e >1. Беручи до уваги, що с2 = а2 + b2, дістаємо:
, але с > a і e >1. Беручи до уваги, що с2 = а2 + b2, дістаємо: 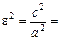
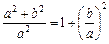 , або
, або 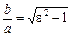 .
.
З останньої рівності випливає, що для гіперболи ексцентриситет характеризує ступінь нахилу віток гіперболи до осі Ох.
Дві прямі, рівняння яких 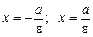 , називаються директрисами еліпса і гіперболи. Для еліпса
, називаються директрисами еліпса і гіперболи. Для еліпса 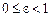 і відношення
і відношення 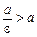 , директриси еліпса — це дві прямі, що розміщені симетрично відносно осі Оу і проходять зовні еліпса. Для гіперболи e > 1 і відношення
, директриси еліпса — це дві прямі, що розміщені симетрично відносно осі Оу і проходять зовні еліпса. Для гіперболи e > 1 і відношення 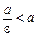 . Тобто директриси гіперболи розміщені симетрично відносно осі Оу і лежать між вітками гіперболи.
. Тобто директриси гіперболи розміщені симетрично відносно осі Оу і лежать між вітками гіперболи.
Для еліпса і гіперболи можна сформулювати важливе твердження: якщо r — відстань від деякої точки еліпса або гіперболи до будь-якого фокуса, а d — відстань від цієї самої точки до директриси, яка відповідає цьому фокусу, то відношення 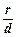 стале й дорівнює ексцентриситету, тобто
стале й дорівнює ексцентриситету, тобто 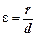 .
.
Розглянуте твердження можна покласти в основу означення цих ліній.
Означення. Множина точок, для яких відношення відстаней від фокуса і до відповідної директриси — величина стала, що дорівнює ексцентриситету e, є еліпс, якщо e < 1, і гіпербола,
якщо e > 1.
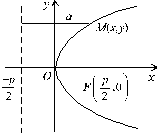 Рис. 5.3
Рис. 5.3
|
Парабола.Означення. Множина точок площини, що містяться на однаковій відстані від даної точки фокуса і даної прямої, яка не проходить через фокус і називається директрисою, є парабола.
За означенням r = d, отже (див. рис. 5.3):
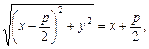 або у2 = 2рх
або у2 = 2рх
— канонічне рівняння параболи, коли e = 1. Парабола симетрична осі Ох, проходить через початок системи координат. Її графік подано на рис. 5.3.
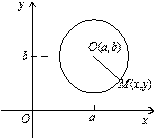 Рис. 5.4
Рис. 5.4
|
Коло.До кривих другого порядку належить і добре відома лінія, яка називається колом (рис. 5.4).
Означення. Множина точок, що містяться на однаковій відстані від
заданої точки — центра, називається колом. За означенням ОМ = R або 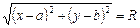 .
.
Піднісши обидві частини рівняння до квадрата, дістанемо:
(х – а)2 + (у – b)2 = R2 (5.4)
— канонічне рівняння кола. Тут (а, b) — координати центра кола, R — його радіус. Розкривши дужки в лівій частині (5.4), дістанемо, очевидно, рівняння другого степеня, тобто коло — також крива другого порядку.
Дата добавления: 2016-05-26; просмотров: 3173;











