Скалярний, векторний і змішаний добуток векторів
Означення. Скалярним добутком двох ненульових векторів 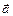 і
і 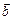 називається число (скаляр), яке дорівнює добутку модулів цих векторів на косинус кута між ними. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.
називається число (скаляр), яке дорівнює добутку модулів цих векторів на косинус кута між ними. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.
Отже:
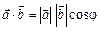 ,
,
де j — кут між векторами. Використовуючи формулу проекції вектора, можна також записати:
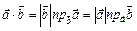 .
.
Властивості скалярного добутку:
1. 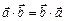 . 4.
. 4. 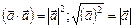 .
.
2. 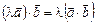 . 5.
. 5. 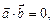 якщо
якщо 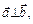 і навпаки,
і навпаки,
3. 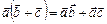 .
. 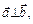 якщо
якщо 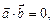
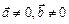 .
.
Нехай вектори 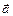 і
і 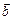 задано за допомогою (2.6), тоді, використовуючи властивості скалярного добутку, умови
задано за допомогою (2.6), тоді, використовуючи властивості скалярного добутку, умови 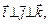 маємо:
маємо:
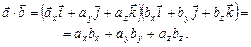 (3.4)
(3.4)
Отже, 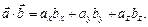
З рівності (2.7) випливає, що:
1. Необхідною і достатньою умовою перпендикулярності векторів 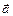 і
і 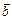 є ах bх + ау bу + аz bz = 0.
є ах bх + ау bу + аz bz = 0.
2. Кут між двома векторами 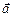 і
і 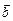 можна знайти за формулою:
можна знайти за формулою:
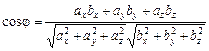 .
.
Означення. Векторним добутком вектора 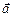 на вектор
на вектор 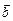 називається вектор
називається вектор 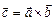 , якщо:
, якщо:
1) довжина вектора 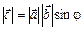 , де j — кут між двома векторами;
, де j — кут між двома векторами;
2) вектор 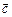 перпендикулярний до кожного з векторів
перпендикулярний до кожного з векторів 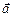 і
і 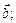
 Рис. 3.2
Рис. 3.2
|
3) вектор 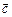 спрямований так, що коли дивитися з його кінця на площину, в якій лежать вектори
спрямований так, що коли дивитися з його кінця на площину, в якій лежать вектори 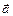 і
і 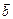 , то поворот вектора
, то поворот вектора 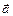 до вектора
до вектора 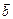 відбувається на найменший кут проти годинникової стрілки.
відбувається на найменший кут проти годинникової стрілки.
Модуль векторного добутку двох неколінеарних векторів дорівнює площі паралелограма, побудованого на векторах як на сторонах.
Властивості векторного добутку:
1. 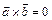 , якщо
, якщо 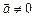 і
і 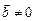 — колінеарні вектори.
— колінеарні вектори.
2. 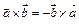 .
.
3. 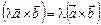 .
.
4. 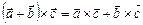 .
.
Знайдемо векторні добутки одиничних векторів 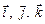 . З колінеарності векторів випливає:
. З колінеарності векторів випливає: 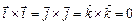 . З того, що одиничні вектори збігаються з напрямом осей прямокутної системи координат, маємо:
. З того, що одиничні вектори збігаються з напрямом осей прямокутної системи координат, маємо:
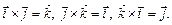
Знайдемо координати вектора 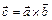 , якщо
, якщо 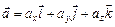 ,
, 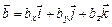 .
.
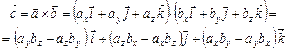 (3.5)
(3.5)
або
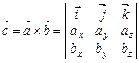 .
.
Означення. Мішаним добутком векторів 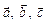 називається число, яке дорівнює скалярному добутку вектора
називається число, яке дорівнює скалярному добутку вектора 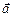 на векторний добуток векторів
на векторний добуток векторів 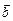 і
і 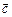 , тобто
, тобто 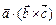 .
.
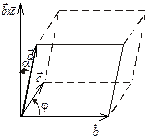 Рис. 3.3
Рис. 3.3
|
Розглянемо геометричний зміст змішаного добутку. Для цього побудуємо на векторах  , вважаючи, що вони не лежать в одній площині, тобто не компланарні, паралелепіпед (рис. 2.9).
, вважаючи, що вони не лежать в одній площині, тобто не компланарні, паралелепіпед (рис. 2.9).
Знайдемо об’єм паралелепіпеда, побудованого на векторах 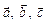 (рис. 2.9). Площа основи його дорівнює модулю векторного добутку векторів
(рис. 2.9). Площа основи його дорівнює модулю векторного добутку векторів 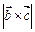
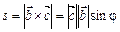 . Висота дорівнює
. Висота дорівнює 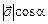 . Отже, остаточно маємо:
. Отже, остаточно маємо:
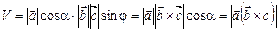 . (3.6)
. (3.6)
З останнього випливає, що модуль мішаного добутку чисельно дорівнює об’єму паралелепіпеда, побудованого на векторах 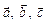 . З рівності (2.9) маємо умову компланарності трьох векторів
. З рівності (2.9) маємо умову компланарності трьох векторів 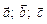 .
.
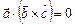 .
.
Ураховуючи формули (2.7) і (2.8) знаходження скалярного і векторного добутків, маємо:
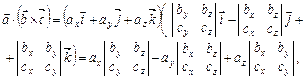
або
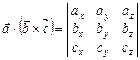 .
.
Властивості мішаного добутку:
1. 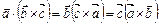 .
.
2. 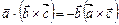 .
.
Дата добавления: 2016-05-26; просмотров: 8357;











