Імпульси, імпульсні послідовності

Аналогові сигнали

Принципи побудови електронних пристроїв, режими роботи приладів залежать від характеру сигналів, які підлягають обробці.

Сигналом називають процес зміни у часі фізичного стану деякого параметру електричного пристрою, який [параметр] використовується для відображення, реєстрації та передачі повідомлень. Повідомлення нерозривно пов’язані з закладеною у них інформацією.

Сигнали, що використовуються в електронній техніці, розділяються на аналогові, дискретні (імпульсні) та цифрові.

Аналогові сигнали описуються неперервними функціями напруги, струму тощо. Джерелами аналогових сигналів є датчики різноманітних фізичних величин. У залежності від характеру зміни, сигнали розділяються на постійні (такі, що повільно змінюються у часі) та змінні. Носієм інформації в постійних сигналах є його рівень відносно нуля напруги чи струму.

Математична модель детермінованого змінного сигналу в загальному вигляді описується формулою:

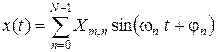, (1.1)

де X_{m, n} , ω_n , φ_n – відповідно, амплітуда, частота та початкова фаза n-ої гармоніки; N – кількість гармонік.

Інформація, що передається сигналом (1.1), як правило, міститься в амплітудах складових. Сигнали (1.1) одержуються та перетворюються (підсилюються), наприклад, у звуковідтворюючій апаратурі. У системах автоматики та радіотехніки часто використовується моногармонічний сигнал:

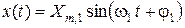, (1.2)

який може використовуватись як базовий для передачі інформації. При цьому інформація, що передається, може міститись у будь-якому з його параметрів – амплітуді, частоті, фазі – або одночасно в декількох з них.

Процес цілеспрямованої зміни параметрів базового сигналу за законом зміни інформації, що передається, називається модуляцією. Базовий сигнал при цьому називається несучим, а функція (1.2) – несучою функцією.

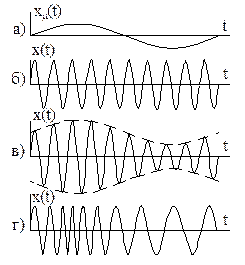
Рис.1.1.

На рис. 1.1, а, б, в ілюструється найпростіший випадок, коли несуча моногармонічна функція x(t) з нульовою початковою фазою та частотою ω₁ модулюється по амплітуді синусоїдальним за формою сигналом x_μ(t) з частотою Ω. Промодульований сигнал, представлений на рис. 1.1, в записується у вигляді:

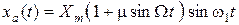, (1.3)

де 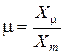– глибина модуляції; X_μ – амплітуда модулюючого сигналу.

Рис. 1.1, г ілюструє зміну базової функції при наявності модуляції по частоті.

Якщо модулюючий сигнал x_μ(t) гармонічний, то модуляція називається гармонічною. Розрізняють амплітудну (АМ), частотну (ЧМ) та фазову (ФМ) модуляції. Останні дві, завдяки взаємозв’язку між частотою та фазою, часто об’єднуються під назвою кутової модуляції.

Пристрої, в яких забезпечується процес модуляції параметрів базової функції, називаються модуляторами.

Описані види модуляції використовуються для передачі сигналів з різних датчиків (наприклад, датчиків рівня рідини у цистернах, температури в приміщеннях і т. п.).

Не вдаючись у деталі теорії модуляції, необхідно відмітити, що амплітудна модуляція більш проста в технічній реалізації, порівняно з кутовими. Але, у той же час, цей вид модуляції має низьку стійкість як відносно зовнішніх перешкод, так і відносно нестабільності параметрів апаратури, в якій вона використовується.

Кутові види модуляції, навпаки, мають достатньо складну технічну реалізацію, але при цьому вони більш стійкі відносно зовнішніх перешкод. Недолік їх полягає в тому, що такі сигнали займають значно ширший частотний спектр порівняно з АМ.

Імпульси, імпульсні послідовності

Підтримувати стабільність і точність параметрів аналогових пристроїв досить важко. На їх роботу впливають технологічні допуски, які закладаються при виробництві електронних компонентів, коливання температури, напруги живлення, космічне випромінювання, шуми і наводки, що створюються електронними приладами, іншими колами і пристроями.

До того ж, реалізація математичних і логічних операцій у більшості випадків або дуже складна, або навіть неможлива при роботі з аналоговими сигналами. Для того, щоб впевнитись у цьому, достатньо спробувати реалізувати на аналогових компонентах будь-яку з відомих констант. Рекомендується провести такий дослід: використовуючи операційний підсилювач і решту реальних компонентів, реалізувати схему підсилювача так, щоб на виході підтримувалась напруга, рівна за величиною числу p = 3,141592653... На практиці забезпечити точність відтворення такого аналогового сигналу навіть з похибкою в 1% досить складно.

Окрім синусоїдальних, в якості базових сигналів часто використовують різні за формою імпульсні послідовності.

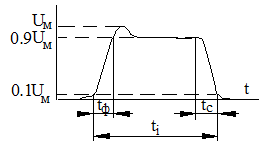
Рис.1.2.

На рис. 1.2 зображений типовий одиночний імпульс та приведені у взаємозв’язку його амплітудні та часові параметри. До амплітудних відносяться: U_м – максимальне значення параметра імпульсу (його амплітуда); ∆U – спад вершини, що визначається між рівнямиU_м і 0,9 U_м ; до часових відносяться: t_ф , t_c – тривалість фронту та спаду імпульсу; t_i– тривалість імпульсу.

Параметри імпульсу в часі можуть змінюватись у широких межах і, відповідно, одиночні імпульси можуть мати різну форму. На рис. 1.3, а – в зображені відповідно експоненціальний, пилоподібний та трикутний імпульси.

Імпульсна послідовність характеризується наявністю пауз між одиночними імпульсами. В якості паузи тривалістю t_п приймається нульовий рівень напруги чи струму або такий рівень, який прирівнюється до нульового (рис. 1.4). Якщо тривалість імпульсів і пауз між ними в послідовності не змінюється, то говорять про періодичну послідовність, яка характеризується періодом

T = t_і + t_п ,

коефіцієнтом заповнення

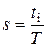
та скважністю

q = s ^{– 1}.

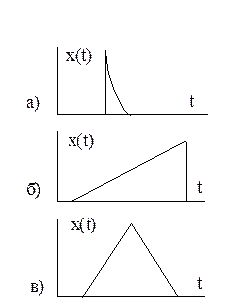Рис.1.3.
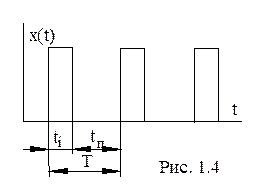
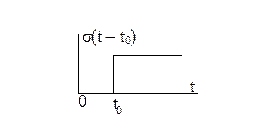Рис.1.5.

У теоретичних дослідженнях часто використовуються ідеалізації імпульсів. Перша з них – це функція включення, або функція Хевісайда. У загальному випадку функція включення, зміщена відносно початку осі координат на величину t₀ (рис. 1.5), записується у вигляді:

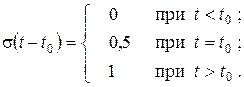(1.4)

У теорії сигналів функції включення широко використовуються для опису розривних та імпульсних сигналів. Імпульсний сигнал прямокутної форми, наприклад, записується так:

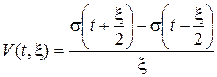. (1.5)

Межа функції V(t, x) при ξ → 0 носить назву дельта-функції, або функції Дірака:

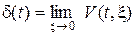. (1.6)

Особливість цього імпульсу полягає в тому, що при будь-якій величині параметру ξйого площа

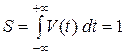(1.7)

залишається незмінною при ξ → 0 .

Іншою особливістю функції Дірака є те, що її розмірність відповідає розмірності частоти.

Для передачі інформації імпульсною послідовністю остання модулюється за аналогією з синусоїдою. У залежності від модульованого параметру, розрізняють модуляції амплітудно-імпульсну (АІМ), широтно-імпульсну (ШІМ), часово-імпульсну, яка поділяється на фазо-імпульсну (ФІМ) і частотно-імпульсну (ЧІМ).

Рис. 1.6 ілюструє особливості модуляції імпульсної послідовності x(t) (рис. 1.6, б) функцією x_μ(t) (рис. 1.6, а) відповідно при АІМ (x_A(t), рис. 1.6, в), ШІМ (x_ш(t), рис. 1.6, г), ЧІМ (x_ч(t), рис. 1.6, д).

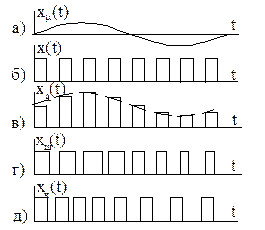
Рис.1.6.

Перевага імпульсних сигналів порівняно з аналоговими полягає у тому, що при однаковій середній потужності імпульсного і аналогового сигналів у першому випадку вся їх енергія концентрується в інтервалі тривалості імпульсу. Тому при коротких імпульсах миттєве значення потужності в імпульсі набагато перевищує її середнє значення. Завдяки цьому відносний вплив зовнішніх факторів на сигнал є значно меншим.

Використання процесів модуляції неможливо без наявності зворотних процесів – виділення інформаційного сигналу з модульованого. Такі процеси називаються демодуляцією або детектуванням.

При передачі інформації часто використовуються операції перетворення неперервного сигналу в імпульсний та навпаки. Ця операція досить наочно ілюструється на рис. 1.6, в.

Для перетворення аналогового сигналу в імпульсну форму необхідно здійснити дискретизацію (квантування) за часом. Це означає, що неперервний час осі t замінюється дискретним з кроком (періодом квантування) Т (рис.1.7).

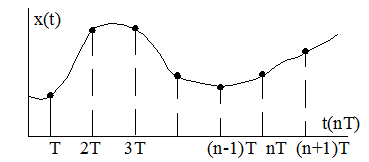
Рис.1.7.

У залежності від способів реалізації дискретизації за часом, сформована імпульсна послідовність може мати різний математичний опис. При перетворенні інформаційних сигналів для цього використовують дельта-функцію (1.6), завдяки особливості її згортки:

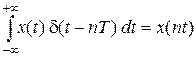. (1.8)

Ця особливість відображає фільтруючу властивість дельта-функції і полягає в тому, що після виконання операцій множення та інтегрування, функція x(t) буде визначеною лише в точках дискретизації за часом nТ (тобто функція визначається з точністю до кроку дискретизації nТ). Функція (1.8) називається дискретною. Величина кроку дискретизації за часом вибирається у відповідності з необхідною точністю відтворення неперервного сигналу. За теоремою В.А. Котельникова, максимальна частота сигналу, який може бути відновлений з дискретної послідовності, не може перевищувати величину

.

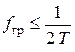Спрощена графічна ілюстрація теореми В.А. Котельникова демонструється рис. 1.8.

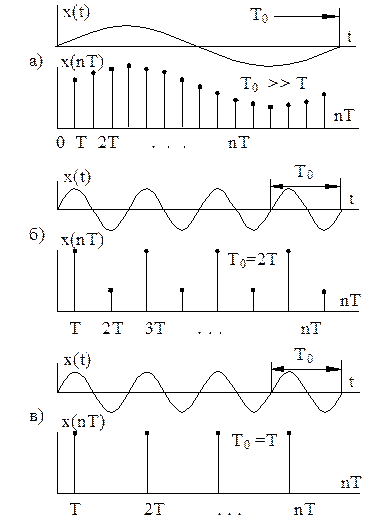
Рис.1.8.

Точність відтворення сигналу з імпульсної послідовності тим вища, чим вища частота дискретизації відносно верхньої частоти спектру інформаційного сигналу. Іншими словами, дискретизація за часом не пов’язана з втратою інформації, якщо частота дискретизації

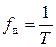
як мінімум у два рази перевищує верхню частоту спектру сигналу f_в . Крок дискретизації T може бути як постійним, так і змінним у залежності від вимог, які ставляться при відновленні сигналу.

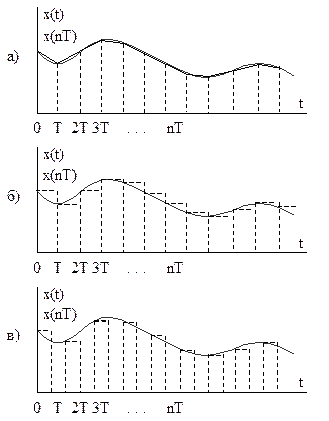
Рис.1.9.

Дискретні значення функції x(nT) можуть використовуватись для відновлення сигналу. Знову ж таки, на практиці використовується широка гама методів відновлення сигналу з квантованої послідовності d-імпульсів. Це може бути лінійна апроксимація (рис. 1.9, а), ступінчаста (рис. 1.9, б) або перетворення в імпульсні послідовності з заданими видами модуляції (рис. 1.9, в).