Взаємне розташування прямих
Дві прямі в просторі можуть співпадати (a 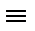 b), бути паралельними (c ll d), перетинатися (m
b), бути паралельними (c ll d), перетинатися (m  n), перехресними
n), перехресними 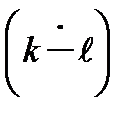 .
.
Якщо дві прямі перетинаються в деякій точці К, то проекції цієї точки повинні належати однойменним проекціям прямих, тобто точки перетину однойменних проекцій прямих, що перетинаються, повинні лежати на одній лінії зв`язку (рис. 1.2.13).
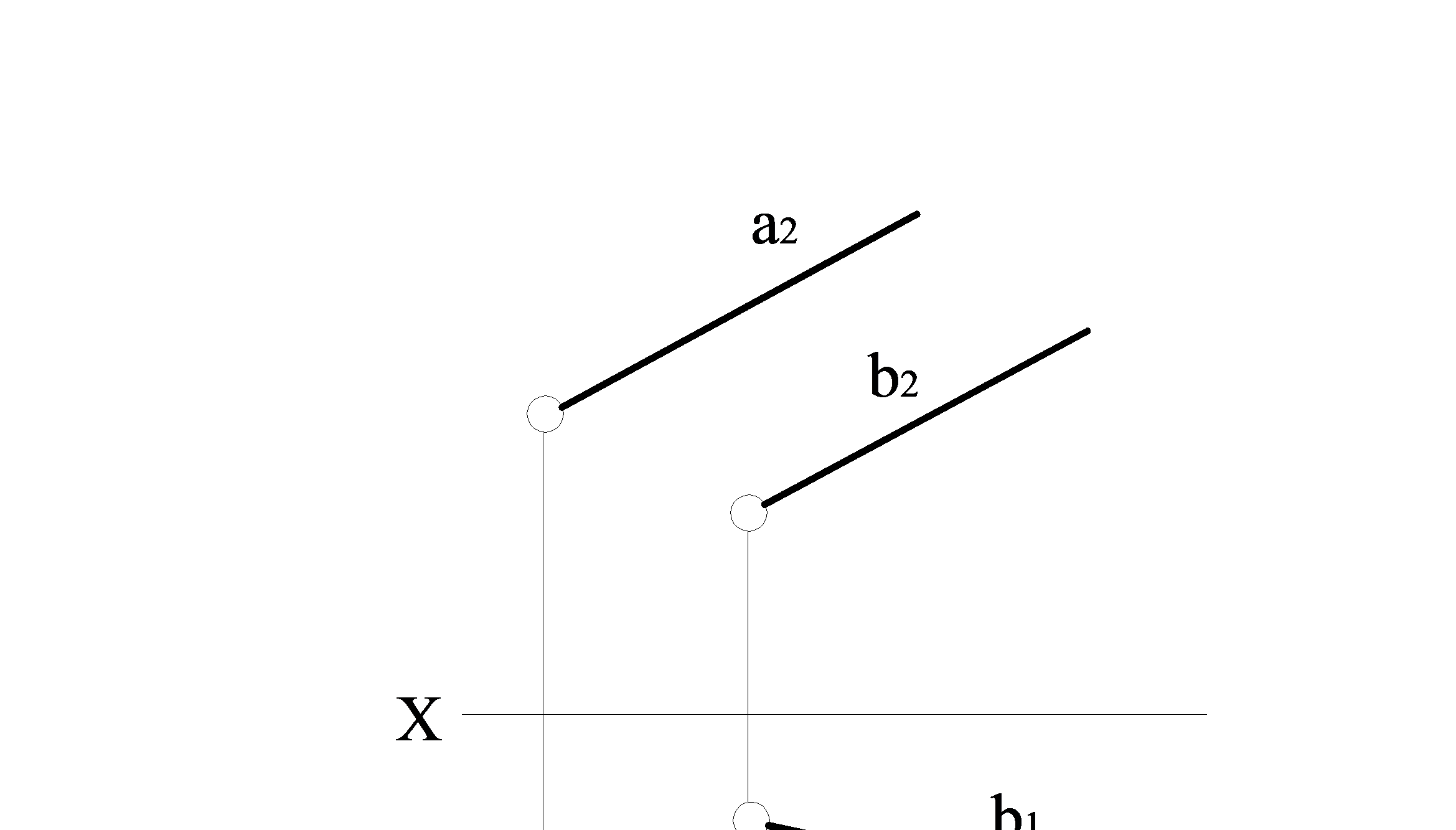
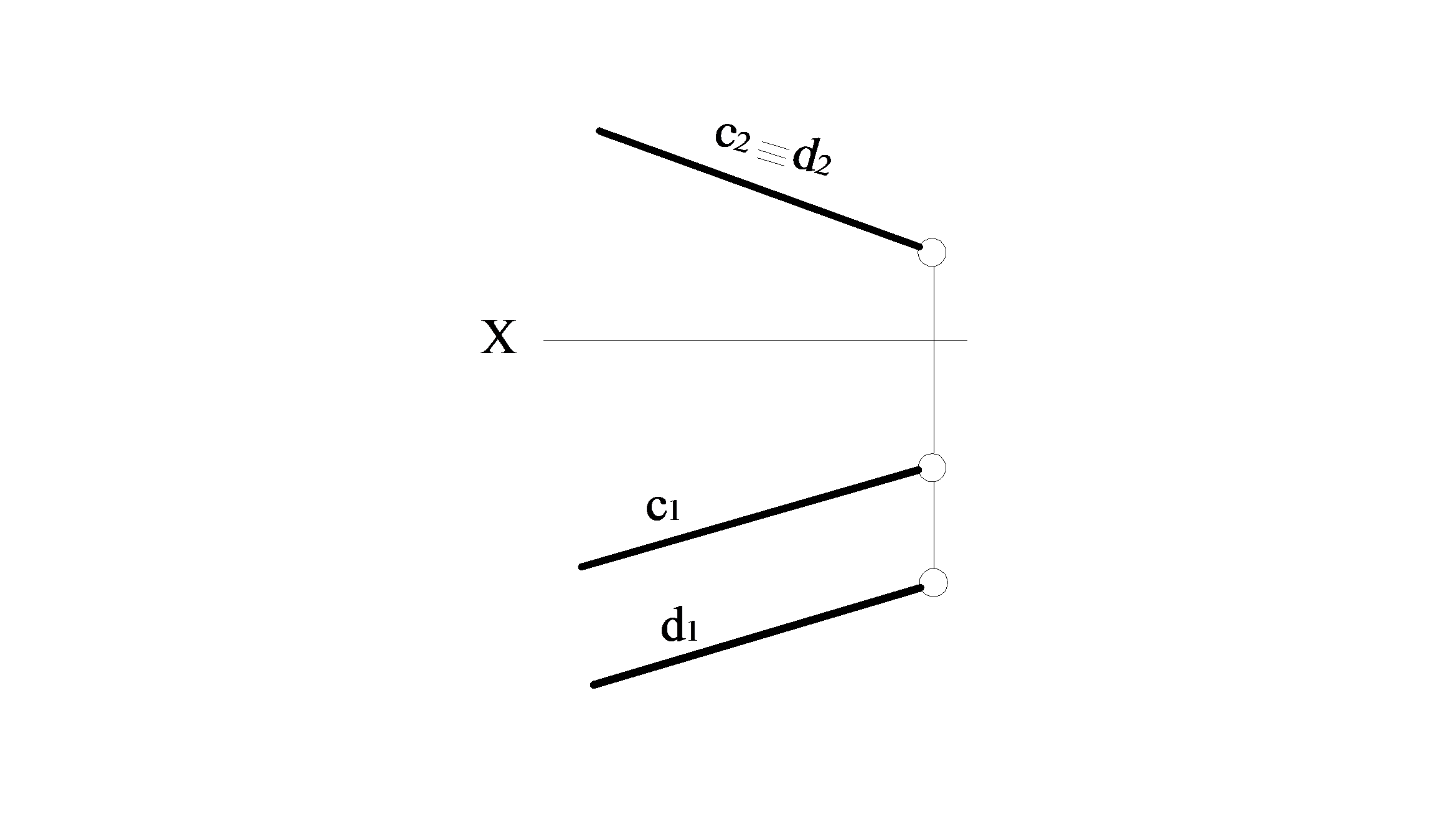
Якщо дві прямі паралельні, то на комплексному кресленні їхні однойменні проекції паралельні (рис. 1.2.14) або збігаються на одній із площин проекцій (рис. 1.2.15).
|
|
Рисунок 1.2.13
|
|
Рисунок 1.2.14
|
|
Рисунок 1.2.15
Якщо прямі паралельні одній з площин проекцій, то їх паралельність визначається на площині, якій прямі паралельні. У наведених нижче прикладах (рис. 1.2.16, рис. 1.2.17) прямі АВ та СD паралельні профільній площині проекцій, таким чином, їх взаємопаралельність визначається на площині П3. На рис. 1.2.16 АВ та СD паралельні між собою, а на рисунку 1.2.17 – не паралельні.
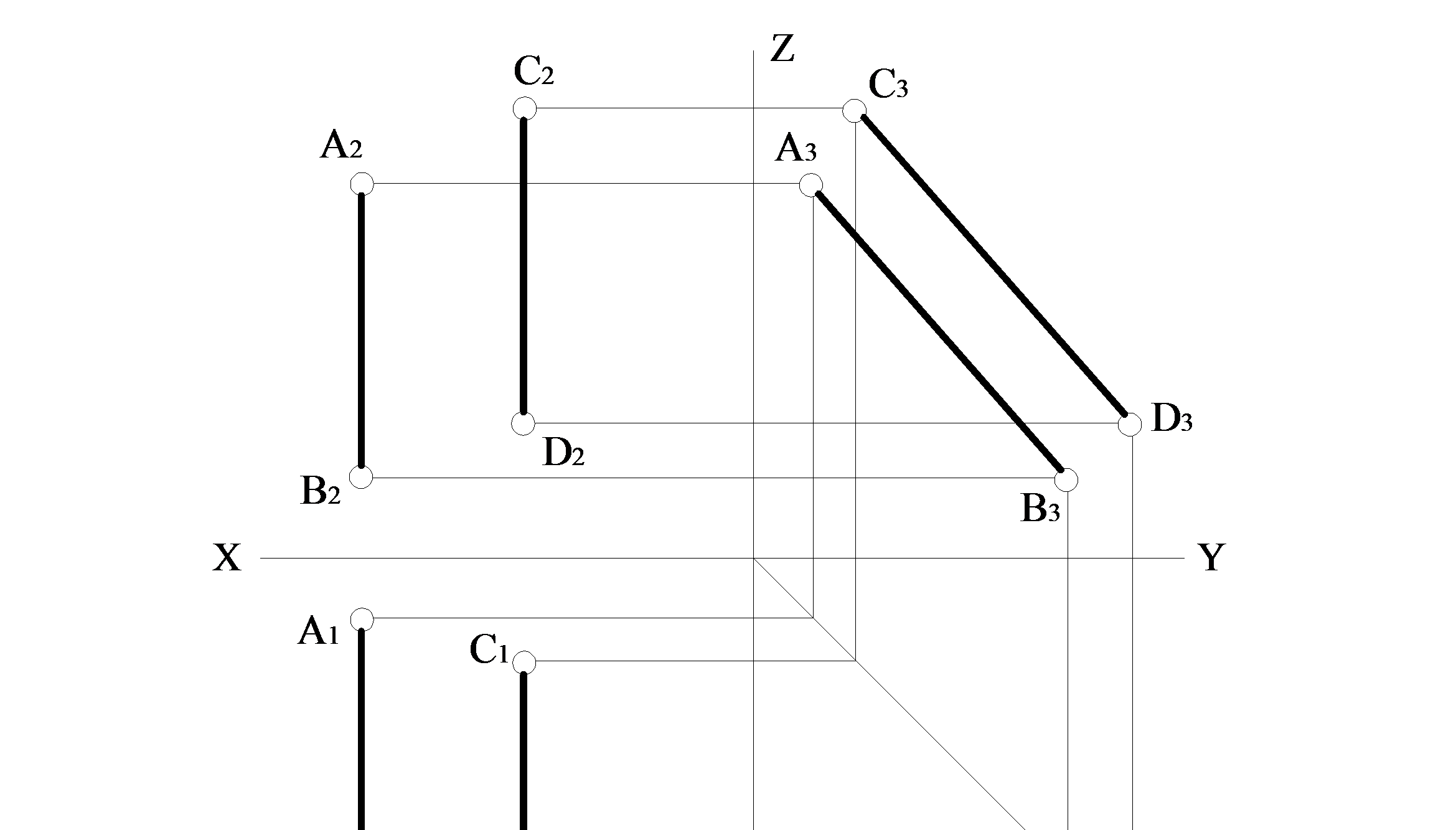
Рисунок 1.2.16
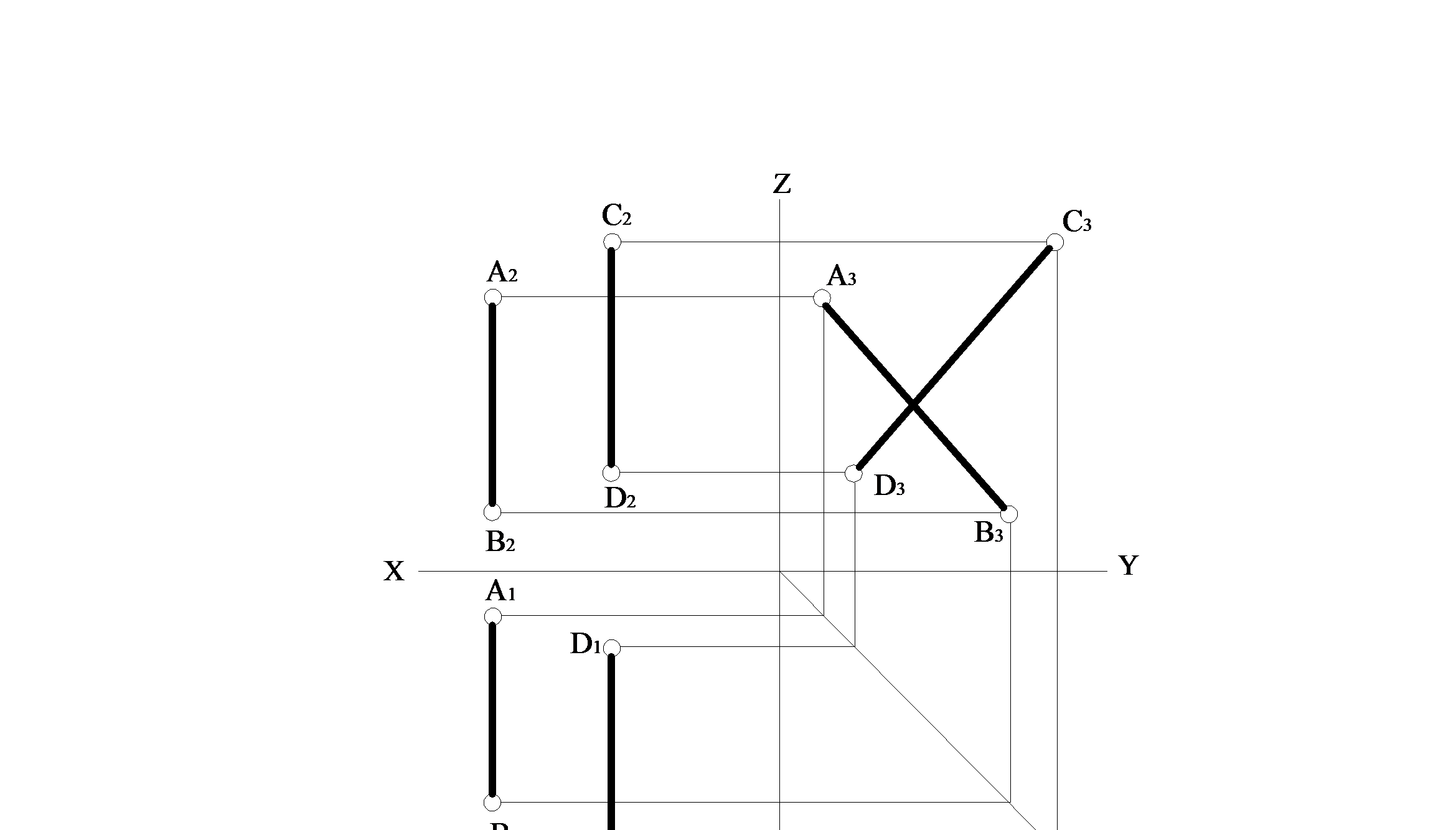
Рисунок 1.2.17
Якщо дві прямі спільних точок не мають і вони не паралельні, то їх називають перехресними.
На рис. 1.2.18 зображено дві перехресні прямі m i n. Фронтальні проекції їх перетинаються в точці 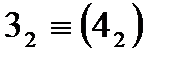 , а горизонтальні – у точці
, а горизонтальні – у точці 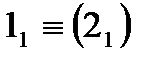 . Для визначення «перекривання» відрізків на проекціях застосовують конкуруючі точки, які лежать на одному проекціювальному промені, належать різним прямим і на одній площині проекцій збігаються.
. Для визначення «перекривання» відрізків на проекціях застосовують конкуруючі точки, які лежать на одному проекціювальному промені, належать різним прямим і на одній площині проекцій збігаються.
На рис. 1.2.18 дві пари конкуруючих точок 1 і 2 відносно поля П1
та 3 і 4 відносно поля П2. При цьому точки 1 і 4 належать відрізку m, а точки 2 і 3 – відрізку n. Оскільки точка 1 розміщена вище від точки 2 на полі П1, то відрізок m «перекриває» відрізок n, невидиму проекцію точки 21 беруть у дужки.
Точка 3 лежить ближче до спостерігача, ніж точка 4, тому на полі П2 відрізок n «перекриває» відрізок m, невидиму проекцію точки 42 беруть у дужки.
На рис. 1.2.19 зображені дві мимобіжні прямі а і b. Фронтальні проекції їх перетинаються в точці 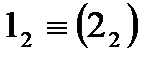 , а на горизонтальній площині проекцій видно, що точка 11 належить а1, а точка 21 належить b1.
, а на горизонтальній площині проекцій видно, що точка 11 належить а1, а точка 21 належить b1.
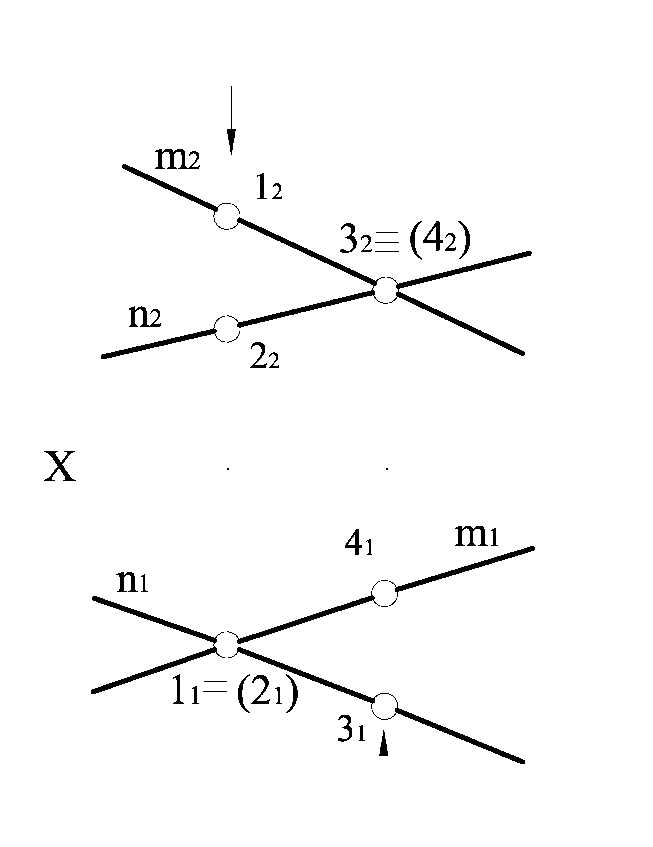 Рисунок 1.2.18
Рисунок 1.2.18
| 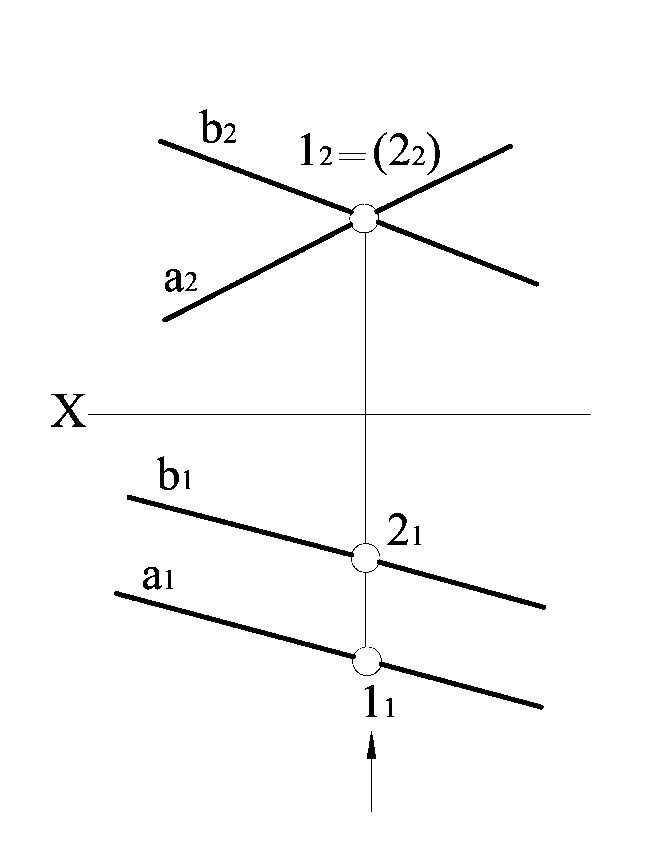 Рисунок 1.2.19
Рисунок 1.2.19
|
Дата добавления: 2016-09-06; просмотров: 2347;

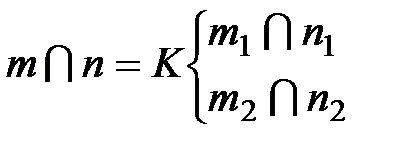
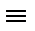 d2
с װ d
c1 װ d1
d2
с װ d
c1 װ d1










