Вероятность успешных (безаварийных) событий

с достоверностью 0,8 при различных значениях r

r n

0,083 0,24 0,418 0,619 0,851

0,056 0,157 0,272 0,394 0,524 0,662 0,813

0,041 0,117 0,201 0,291 0,384 0,481 0,528 0,686 0,798 0,922

Рассмотрим альтернативный подход с привлечением модели, учитывающей некоторые физические процессы, полагая, что авария на взрывоопасном объекте возникает в результате накопления элементарных повреждений у при достижении некоторого предельно допустимого износа М. Процесс накопления повреждений фиксируется функцией износа ɳ(t). Отказ наступает при условии ɳ(t)≥M числе элементарных повреждений r=M/y. Такая модель называется «стареющей системой».

Расчет вероятности отказа (аварии) возможен с использованием модели монотонно стареющих систем, т.е. с накапливающимися повреждениями, на основе гамма-распределения:

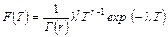, (4.18)

где Г(r) - гамма-функция; 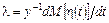- скорость износа.

Для целых значений r гамма-функция Г(r)=(r –1)!, λ- средняя скорость износа и функция гамма-распределения имеет вид:

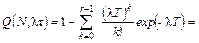
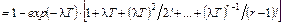(4.19)

При r=1 выражение (4.19) соответствует плотности экспоненциального распределения (мгновенный выход из строя при однократном повреждении). Приведем примеры оценки риска аварий.

Пример 1. Расчет риска аварии по модели «высоконадежных систем».

Задание: На опасном производственном объекте за 20 лет произошло 4 аварии. Оценить вероятность возникновения двух аварий (N=2) в течение двух лет (t=2); вероятность безаварийной работы в течение года.

Решение.

1. Определим интенсивность отказа оборудования и параметр λt:

λ = 4/20 =0,2 лет^-1

λt = 0,2·2 = 0,4

2. Находим искомую вероятность Q (N, λt) двух аварий по распределению Пуассона:

Q (2;0,4) = (0,2·2)²·е^–0,4/2!=0,054,

3. Проводим расчет безаварийной работы (N=0, λt = 0,2):

Q (0;0,2) = е^–0,2= 0,82.

Пример 2. Расчет взрыва трубопровода с газом по модели «стареющей системы»

Задание: Средняя скорость износа λ трубопровода с взрывоопасным газом составляет 0,02 ч^-1. Предельное число повреждений, после которых наступит взрыв, равно r = 6. Определить риск аварии в течение недели, если трубопровод работает три часа в день.

Решение.

1. Определяем срок работы трубопровода и параметр λt:

t = 3·7 = 21 час;

λt = 21·0,02= 0,42

2. Проводим расчет риска взрыва трубопровода:

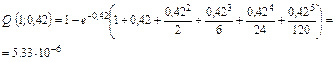
Пример 3. Провести расчет риска взрыва трубопровода по модели стареющей системы, если число предельных повреждений равно 1 (r = 1). См. условие примера 2.

Решение.

Проводим расчет риска, если N=1:

Q (1;0,42) = 1 – е^–04,2·(1+0,42) =6,7·10^-2

Рассмотренные методологические подходы позволяют произвести количественную оценку степени безопасности населения, проживающего в районе расположения ПОО, и расчет ежегодных платежей за риск в страховой фонд ЧС. Кроме того, выполненное по специальной методике картирование риска позволяет идентифицировать все места возможного скопления большого числа лиц на территории вероятного поражения и определить количество смертельных исходов в год в зонах недопустимо высокого риска R(L)>10^-5.

<27 28 293031 32 33 >

Дата добавления: 2020-06-09; просмотров: 481;

Поиск по сайту

Узнать еще