Оценка риска аварий по различным моделям
Прогнозирование аварийных ситуаций возможно на основе элементарной статистики и дискретного распределения Пуассона, часто применяемого к редким событиям и природным явлениям. Такую модель называют «высоконадежной системой». Функцией риска аварии из-за отказа нормального функционирования объекта называется вероятность отказа:
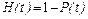 (4.8)
(4.8)
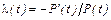 (4.9)
(4.9)
где P(t) - вероятность безотказной работы (функция надежности), λ(t) - интенсивность отказов, равная вероятности того, что после безотказной работы до момента времени t авария произойдет в последующем малом отрезке времени. Опыт показывает, что после небольшого начального периода эксплуатации (приработки) функция λ(t) длительный период достаточно стабильна, т.е. λ(t) = const. Влияние интенсивного старения за счет коррозионного износа, усталости и других факторов должно исключаться регламентированием допустимого срока службы.
Принимая для периода нормального (спокойного) функционирования λ(t)=const, получаем экспоненциальное распределение:
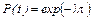 (4.10)
(4.10)
Здесь 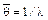 - математическое ожидание срока службы (ресурса) или средняя наработка на отказ. Функцию риска Н(t) можно записать в виде:
- математическое ожидание срока службы (ресурса) или средняя наработка на отказ. Функцию риска Н(t) можно записать в виде:
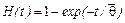 (4.11)
(4.11)
Частота отказов в системе однотипных объектов (поток случайных событий) соответствует дискретному распределению Пуассона:
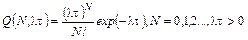 (4.12)
(4.12)
Согласно данной формуле, аварии на временном интервале τ(t,t+τ) произойдут N раз с вероятностью Q(N,λτ), а отсутствие аварийных ситуаций (отсутствие отказов) – с вероятностью:
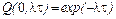 (4.13)
(4.13)
Вероятность того, что аварии произойдут п раз при п < N (т.е. менее N раз), определяется функцией распределения:
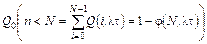 , (4.14)
, (4.14)
где 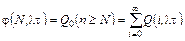
Вероятность возникновения хотя бы одной аварии представляет оценку риска аварий 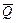 на объекте в период τ:
на объекте в период τ:
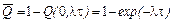 (4.15)
(4.15)
Значения вероятности аварий Q(N,λτ) и риска возможной аварии 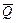 для числа N ≤ 5 приведены в табл. 4.6.
для числа N ≤ 5 приведены в табл. 4.6.
Таблица 4.6
Вероятность N аварий и оценка риска аварийности Q
в зависимости от параметра λτ согласно распределению Пуассона
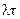 N
N
| 0,1 | 0,2 | 0,3 | 0,5 | |||||
| 0,905 | 0,819 | 0,741 | 0,607 | 0,368 | 0,135 | 0,05 | 0,01 | 0,007 | |
| 0,091 | 0,164 | 0,222 | 0,303 | 0,368 | |||||
| 0,0045 | 0,016 | 0,033 | 0,013 | 0,061 | 0,271 | ||||
| 0,0002 | 0,0011 | 0,0033 | 0,013 | 0,061 | 0,18 | 0,224 | |||
| 0,0001 | 0,0003 | 0,0016 | 0,015 | 0,09 | 0,168 | 0,195 | |||
| 0,0002 | 0,003 | 0,036 | 0,101 | 0,156 | 0,176 | ||||
| 0,095 | 0,181 | 0,259 | 0,393 | 0,632 | 0,865 | 0,95 | 0,982 | 0,993 |
Распределение Пуассона является частным случаем биноминального распределения при большом числе маловероятных событий. В связи с этим формулу Пуассона называют законом редких явлений. При больших значениях λτ(λτ≥10)распределение приближается к нормальному распределению при μ=σ2=λτ:
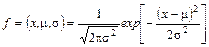 (4.16)
(4.16)
Распределение Пуассона используется на практике в различных областях техники и природных процессах. Распределение Пуассона применимо также к событиям (авариям), разбросанным на площадях. В этом случае параметр λ имеет смысл средней плотности, отнесенной не к временному интервалу, а к некоторой площади.
Оценку надежности производственных участков и различной аппаратуры, а также обслуживания персоналом можно провести с использованием биноминального распределения подсчетом вероятности как частоты r успешных событий при их общем числе п. Доверительный интервал для фактической вероятности РT определяется уравнением:
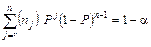 , (4.17)
, (4.17)
где 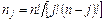 – биноминальные коэффициенты; Р - нижняя граница искомой надежности РТ; α - достоверность того, что фактическая вероятность РТ находится в интервале Р...1.
– биноминальные коэффициенты; Р - нижняя граница искомой надежности РТ; α - достоверность того, что фактическая вероятность РТ находится в интервале Р...1.
Таблица 4.7
Дата добавления: 2020-06-09; просмотров: 648;











