Дискретное преобразование Фурье
Дискретное преобразование Фурье есть частный вид преобразования Фурье, когда последовательность имеет конечную длительность.
Рассмотрим сначала ряды Фурье периодических последовательностей. Пусть 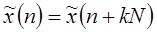 . Такие последовательности не могут быть представлены z-преобразованием, так как не существует ни одного значения z, для которого бы сходилось z-преобразование такой последовательности. Однако можно представить
. Такие последовательности не могут быть представлены z-преобразованием, так как не существует ни одного значения z, для которого бы сходилось z-преобразование такой последовательности. Однако можно представить 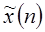 рядом Фурье, т.е. суммой комплексных экспонент с частотами, кратными основной частоте
рядом Фурье, т.е. суммой комплексных экспонент с частотами, кратными основной частоте 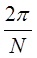 периодической последовательности. В противоположность рядам Фурье непрерывных периодических функций имеется только N различных комплексных экспонент с периодом, равным целой части основного периода N. Это является следствием того, что комплексная экспонента
периодической последовательности. В противоположность рядам Фурье непрерывных периодических функций имеется только N различных комплексных экспонент с периодом, равным целой части основного периода N. Это является следствием того, что комплексная экспонента 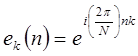 периодична по k с периодом N, т.е.
периодична по k с периодом N, т.е. 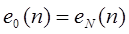 ,
, 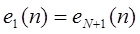 и т.д., следовательно, множество N комплексных экспонент с k=0,1,2…N-1 определяет все различные комплексные экспоненты с частотами, кратными
и т.д., следовательно, множество N комплексных экспонент с k=0,1,2…N-1 определяет все различные комплексные экспоненты с частотами, кратными 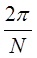 . Поэтому представление периодической последовательности
. Поэтому представление периодической последовательности 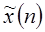 в виде ряда Фурье содержит только N этих комплексных экспонент и, следовательно, имеет вид
в виде ряда Фурье содержит только N этих комплексных экспонент и, следовательно, имеет вид
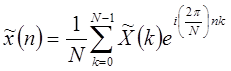 . .
| (1.46) |
Коэффициенты 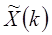 в (1.46) получаются из соотношения
в (1.46) получаются из соотношения
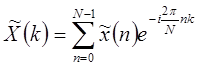
| (1.47) |
Выражения (1.46) и (1.47) могут рассматриваться как пара преобразований Фурье. Введем обозначение 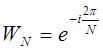 . Тогда ДРФ (дискретный ряд Фурье) пары представляются в виде:
. Тогда ДРФ (дискретный ряд Фурье) пары представляются в виде:
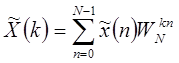
| (1.48) |
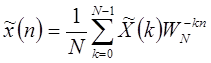
| (1.49) |
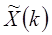 можно интерпретировать как равноудаленные по углу выборки z-преобразования одного периода
можно интерпретировать как равноудаленные по углу выборки z-преобразования одного периода 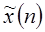 , взятые на единичной окружности.
, взятые на единичной окружности.
Теперь перейдем к рассмотрению последовательностей конечной длины. Преобразование последовательности конечной длины будем называть дискретным преобразованием Фурье.
Мы можем представить последовательность конечной длины N-периодической последовательностью периода N, один период которой совпадает с данной последовательностью. В этом случае исходная последовательность имеет такое же ДРФ представление, что и периодическая последовательность. Т.е. 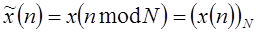 . Последовательность конечной длины
. Последовательность конечной длины 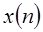 получается из
получается из 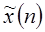 выделением одного периода, т.е.
выделением одного периода, т.е. 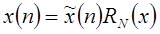 , где
, где 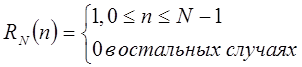 . То же самое можно записать и для выражений в частотной области:
. То же самое можно записать и для выражений в частотной области: 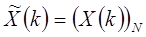 ;
; 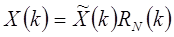 .
.
Тогда
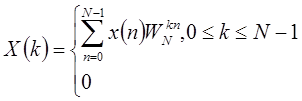
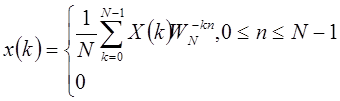
| (1.50) |
Пара соотношений, определяемая преобразованиями (1.50) будет называться дискретным преобразованием Фурье. Отметим, что ДРФ последовательности конечной длины соответствует равноудаленным выборкам из z-преобразования на единичной окружности. Нужно подчеркнуть, что различие между последовательностью конечной длины и периодической последовательностью длины N невелико в том смысле, что обе они определяются N значениями и поэтому различия между (1.48) и (1.50) не столь велики.
Дискретное преобразование Фурье обладает свойством линейности.
Ранее было показано, что умножение коэффициентов ДРФ двух последовательностей соответствует периодической свертке этих последовательностей. Рассмотрим последовательности 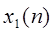 и
и 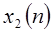 конечной длительности N с ДПФ
конечной длительности N с ДПФ 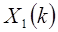 и
и 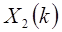 , и определим последовательность
, и определим последовательность 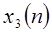 , для которой коэффициенты ДПФ равны
, для которой коэффициенты ДПФ равны 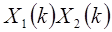 .
.
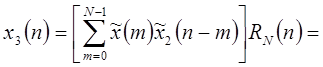
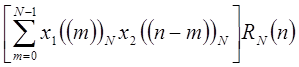
| (1.51) |
Выражение (1.51) отличается от линейной свертки 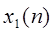 и
и 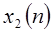 . Для линейной свертки основные операции включают умножение
. Для линейной свертки основные операции включают умножение 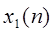 на обращенную во времени и линейно сдвинутую копию
на обращенную во времени и линейно сдвинутую копию 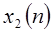 , а также суммирование значений произведений. Чтобы получить значение свертки, эти последовательности сдвигаются по отношению друг к другу. В противоположность этому для свертки по (1.51) следует представить, что одна из последовательностей расположена на поверхности цилиндра в N равноудаленных точках. Вторая последовательность обращается во времени и также располагается на поверхности цилиндра в N точках. Если вообразить, что один цилиндр помещен внутрь другого, то тогда значение свертки может быть получено путем умножения значений на одном цилиндре на соответствующие значения на другом цилиндре и суммирования полученных произведений. Такая свертка часто называется круговой.
, а также суммирование значений произведений. Чтобы получить значение свертки, эти последовательности сдвигаются по отношению друг к другу. В противоположность этому для свертки по (1.51) следует представить, что одна из последовательностей расположена на поверхности цилиндра в N равноудаленных точках. Вторая последовательность обращается во времени и также располагается на поверхности цилиндра в N точках. Если вообразить, что один цилиндр помещен внутрь другого, то тогда значение свертки может быть получено путем умножения значений на одном цилиндре на соответствующие значения на другом цилиндре и суммирования полученных произведений. Такая свертка часто называется круговой.
В большинстве случаев нас интересует линейная свертка двух последовательностей. Рассмотрим сначала две N-точечные последовательности 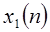 и
и 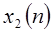 , и обозначим
, и обозначим 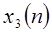 их линейную свертку, т.е.
их линейную свертку, т.е. 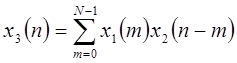 . Непосредственно проверяется, что
. Непосредственно проверяется, что 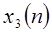 имеет длину 2N-1, т.е. она может иметь самое большое 2N-1 ненулевых точек. Если она вычисляется после умножения дискретных преобразований Фурье
имеет длину 2N-1, т.е. она может иметь самое большое 2N-1 ненулевых точек. Если она вычисляется после умножения дискретных преобразований Фурье 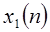 и
и 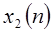 , тогда каждое из этих преобразований Фурье
, тогда каждое из этих преобразований Фурье 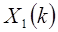 и
и 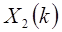 должно вычисляться на основе 2N-1 точек.
должно вычисляться на основе 2N-1 точек.
Поэтому, если определить
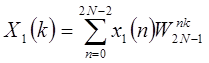 ; ; 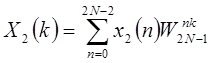
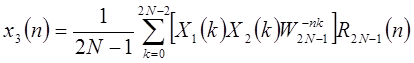 , ,
| (1.52) |
то 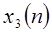 будет линейной сверткой
будет линейной сверткой 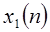 и
и 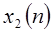 .
.
Дата добавления: 2020-06-09; просмотров: 795;











