Представление дискретных сигналов и систем в частотной области.
В установившемся состоянии отклик линейной стационарной системы на синусоидальный сигнал является синусоидой той же частоты с амплитудой и фазой, определяемыми системой.
Чтобы убедиться в справедливости этого для дискретных систем, предположим, что входная последовательность является комплексной экспонентой круговой частоты 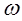 ,
, 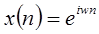 .
.
Тогда получим выходной сигнал:
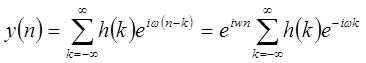
| (1.20) |
Если ввести
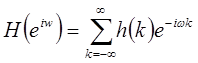 , ,
| (1.21) |
то можно записать
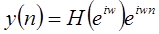
| (1.22) |
Отсюда видно, что 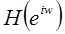 описывает изменение комплексной экспоненты как функции частоты
описывает изменение комплексной экспоненты как функции частоты 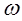 . Величина
. Величина 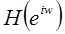 называется частотной характеристикой системы.
называется частотной характеристикой системы.
Поскольку синусоиду можно представить как линейную комбинацию комплексных экспонент, то частотная характеристика также выражает отклик на синусоидальный сигнал. А именно, рассмотрим
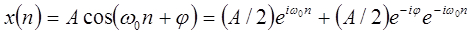
| (1.23) |
Из (1.22) отклик на 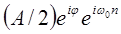 равен
равен 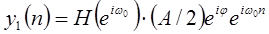 . Если
. Если 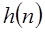 действительная функция, то отклик на
действительная функция, то отклик на 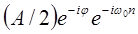 является комплексно-сопряженным откликом на
является комплексно-сопряженным откликом на 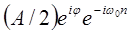 . Поэтому результирующий отклик равен
. Поэтому результирующий отклик равен
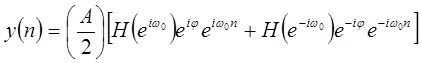
| (1.24) |
или
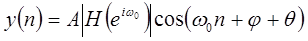 , ,
| (1.25) |
где 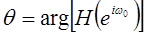 - значение фазочастотной характеристики.
- значение фазочастотной характеристики.
Частотная характеристика 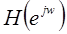 является непрерывной функцией частоты. Кроме того, это периодическая функция частоты с периодом
является непрерывной функцией частоты. Кроме того, это периодическая функция частоты с периодом 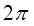 . Это свойство следует непосредственно из (1.22), так как
. Это свойство следует непосредственно из (1.22), так как 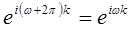 . То, что частотная характеристика имеет одинаковые значения на частотах
. То, что частотная характеристика имеет одинаковые значения на частотах 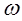 и
и 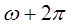 , означает, что система реагирует одинаково на комплексные экспоненты этих двух частот. Такое поведение понятно, так как эти две экспоненциальные последовательности совпадают друг с другом.
, означает, что система реагирует одинаково на комплексные экспоненты этих двух частот. Такое поведение понятно, так как эти две экспоненциальные последовательности совпадают друг с другом.
Поскольку 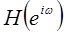 - периодическая функция частоты, она может быть представлена в виде ряда Фурье. Фактически (1.22) и представляет
- периодическая функция частоты, она может быть представлена в виде ряда Фурье. Фактически (1.22) и представляет 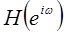 в виде ряда Фурье, в котором коэффициентами Фурье являются значения импульсной характеристики
в виде ряда Фурье, в котором коэффициентами Фурье являются значения импульсной характеристики 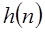 . Отсюда следует, что
. Отсюда следует, что 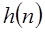 могут быть определены через
могут быть определены через 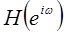 как коэффициенты Фурье периодической функции, т.е.
как коэффициенты Фурье периодической функции, т.е.
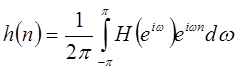 , ,
| (1.26) |
где
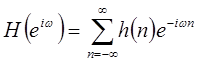 . .
| (1.27) |
Таким образом, (1.26) и (1.27) являются парой преобразований Фурье для последовательности 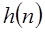 , где (1.27) играет роль прямого, а (1.26) обратного преобразования Фурье. Такое представление существенно только тогда, когда (1.27) сходится.
, где (1.27) играет роль прямого, а (1.26) обратного преобразования Фурье. Такое представление существенно только тогда, когда (1.27) сходится.
Для произвольной последовательности 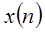 определим преобразование Фурье соотношением:
определим преобразование Фурье соотношением:
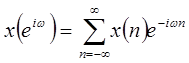 , ,
| (1.28) |
а обратное преобразование Фурье соотношением:
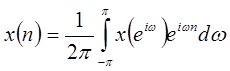 . .
| (1.29) |
Ряды (1.28) не всегда сходятся. Имеются различные определения и интерпретации сходимости преобразования Фурье. Если 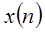 абсолютно суммируема, т.е. если
абсолютно суммируема, т.е. если 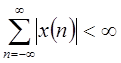 , то ряд называется абсолютно сходящимся и сходится равномерно к непрерывной функции
, то ряд называется абсолютно сходящимся и сходится равномерно к непрерывной функции 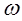 .
.
Если рассматривать (1.29) как суперпозицию комплексных экспонент бесконечно малой амплитуды, то отклик на 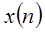 является суперпозицией откликов на каждую экспоненту, входящую в представление сигнала
является суперпозицией откликов на каждую экспоненту, входящую в представление сигнала 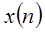 . Так как отклик на каждую комплексную экспоненту получается умножением на
. Так как отклик на каждую комплексную экспоненту получается умножением на 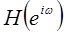 , то
, то
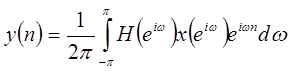 . .
| (1.30) |
Поэтому преобразование Фурье выходного сигнала равно
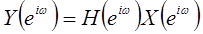 . .
| (1.31) |
Этот результат имеет свой аналог в теории линейных систем с непрерывным временем и может быть получен более строгим образом путем применения преобразования Фурье к свертке
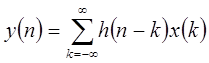 . .
| (1.32) |
Пример. Идеальный фильтр нижних частот с дискретным временем
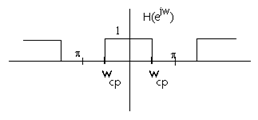 Рис. 1.1.
Рис. 1.1.
| имеет частотную характеристику 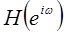 , вид которой изображен на рисунке Рис. 1.1. , вид которой изображен на рисунке Рис. 1.1.
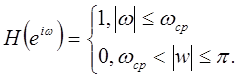
|
Так как 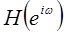 является периодической функцией, то это соотношение определяет частотную характеристику для всех
является периодической функцией, то это соотношение определяет частотную характеристику для всех 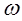 .
.
Такая система удаляет из входного сигнала все компоненты в диапазоне частот 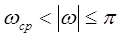 .
.
Импульсная характеристика 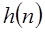 определяется следующим образом:
определяется следующим образом:
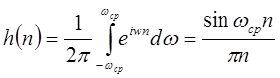
| (1.33) |
Идеальный фильтр нижних частот является примером системы, которая очень эффективно описывается в частотной области. Легко видеть, что эта система полностью удаляет из входного сигнала компоненты с частотой выше частоты среза 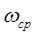 . Ясно, что идеальный фильтр нижних частот не является физически реализуемой системой.
. Ясно, что идеальный фильтр нижних частот не является физически реализуемой системой.
Дата добавления: 2020-06-09; просмотров: 824;











