Дискретизация сигналов с непрерывным временем
Часто дискретные сигналы получаются из аналоговых сигналов с помощью периодической дискретизации.
Рассмотрим аналоговый сигнал 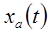 , имеющий представление Фурье:
, имеющий представление Фурье:
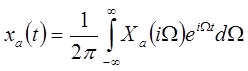
| (1.34) |
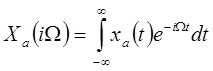
| (1.35) |
Говорят, что последовательность 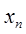 со значениями
со значениями 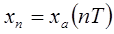 получена из
получена из 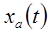 периодической дискретизацией, а
периодической дискретизацией, а 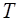 называется периодом дискретизации. Чтобы определить в каком смысле
называется периодом дискретизации. Чтобы определить в каком смысле 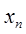 представляет исходный сигнал
представляет исходный сигнал 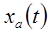 с
с 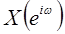 преобразованием Фурье последовательности
преобразованием Фурье последовательности 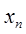 .
.
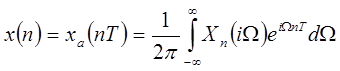
| (1.36) |
Преобразование Фурье в дискретном времени также дает представление
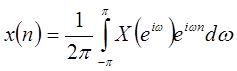
| (1.37) |
Путем замены (1.36) на сумму интегралов по интервалам длиной 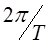 можно получить:(3.1)
можно получить:(3.1)
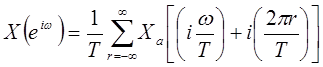
| (1.38) |
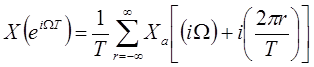
| (1.39) |
Из соотношений (1.38) и (1.31) становится совершенно ясной связь между преобразованием Фурье в непрерывном времени и преобразованием Фурье последовательности, полученной посредством дискретизации.
Если период дискретизации слишком велик, сдвинутые варианты спектра 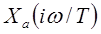 перекрываются. В этом случае верхние частоты
перекрываются. В этом случае верхние частоты 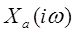 отражаются в более низкие частоты
отражаются в более низкие частоты 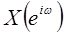 .
.
На нижнем рисунке спектральные свойства исходного сигнала тиражированы бесконечное число раз, поэтому можно ожидать, что 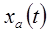 может быть восстановлено по выборкам может быть восстановлено по выборкам 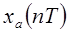 при помощи подходящей интерполяционной формулы. Отсюда ясно, что наименьшая частота дискретизации должна удовлетворять неравенству при помощи подходящей интерполяционной формулы. Отсюда ясно, что наименьшая частота дискретизации должна удовлетворять неравенству 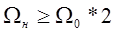 . Эта частота дискретизации часто называется частотой Найквиста. . Эта частота дискретизации часто называется частотой Найквиста.
| 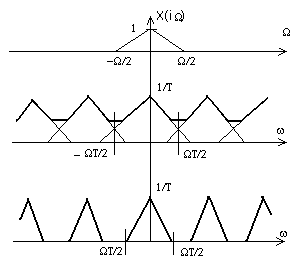 Рис. 1.2.
Рис. 1.2.
|
Z-преобразование
В теории систем с непрерывным временем преобразование Лапласа может рассматриваться как обобщение преобразования Фурье. Подобным образом можно обобщить преобразование Фурье для дискретных сигналов и систем на основе z-преобразования.
Z-преобразование используется при анализе дискретных линейных стационарных систем. Прямое z-преобразование
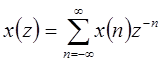
| (1.40) |
где z-комплексная переменная (сравнить с преобразованием Фурье 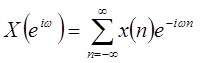 ).
).
Представив z в полярных координатах 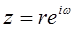 , получаем
, получаем
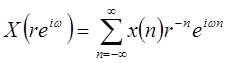
| (1.41) |
Поэтому z-преобразование можно интерпретировать как преобразование Фурье последовательности x(n), умноженное на экспоненциальную последовательность.
Z-преобразование сходится не для всех последовательностей и не для всех z. Для любой последовательности множество тех значений z, для которых z-преобразование сходится, называется областью сходимости.
Важный класс z-преобразований представляют преобразования 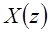 , являющиеся рациональными функциями, т.е. отношениями полиномов от z. При этом корни числителя называют нулями, а корни знаменателя – полюсами. Область сходимости z-преобразования ограничена полюсами.
, являющиеся рациональными функциями, т.е. отношениями полиномов от z. При этом корни числителя называют нулями, а корни знаменателя – полюсами. Область сходимости z-преобразования ограничена полюсами.
Пример. Рассмотрим последовательность 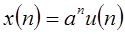 (
( 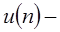 «ступенька»). Ее z-преобразование задается рядом
«ступенька»). Ее z-преобразование задается рядом 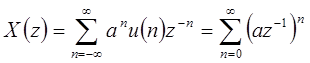 , который сходится к
, который сходится к 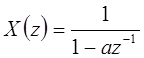 для
для 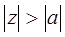 , имеет нуль в точке
, имеет нуль в точке 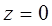 и полюс в точке
и полюс в точке 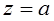 .
.
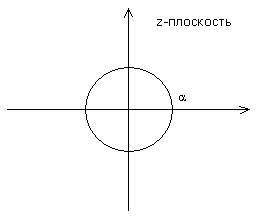 Рис. 1.3.
Рис. 1.3.
| Можно показать, что для правосторонней последовательности ( 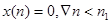 ) областью сходимости является внешняя область круга. Для левосторонней последовательности областью сходимости является внутренность круга. ) областью сходимости является внешняя область круга. Для левосторонней последовательности областью сходимости является внутренность круга.
|
Дата добавления: 2020-06-09; просмотров: 872;











