Свойства общего решения
1) Т.к. постоянная С – произвольная величина, то, вообще говоря, дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0).
Частным решением дифференциального уравнения называется решение, полученное из общего решения при фиксированных значениях постоянной.
Задачей Кошиназывается нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши(теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную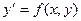 
, то какова бы не была точка (х0, у0) в области D, существует единственное решение 
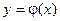уравнения 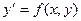, определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.е. существует единственное решение дифференциального уравнения.
Пример. Найти общее решение дифференциального уравнения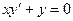 
.
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
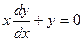
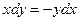
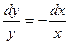
Теперь интегрируем: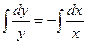 
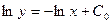
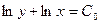
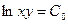
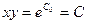
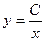- общее решение исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
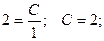
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
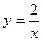
Дата добавления: 2020-06-09; просмотров: 399;
Поиск по сайту
Узнать еще
- ОСНОВНЫЕ ТИПЫ И СВОЙСТВА НАПОЛЬНЫХ И БОРТОВЫХ СИСТЕМ ТЕХНИЧЕСКОГО ДИАГНОСТИРОВАНИЯ
- I. Товар и его свойства.
- II.3. Физико-химические свойства нефтей и природных газов
- II.4. Классификация нефтей и газов по их химическим и физическим свойствам
- X. Электроповерхностные свойства дисперсных систем
- А) Определяется механическими и тепловыми свойствами
- Абстрактные автоматы. Методы описания и свойства
- Акустические свойства голоса
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
