Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение первого порядка у′ = f(x, y) называется уравнением с разделяющимися переменными, если его можно представить в виде:
у′ = f1(x) ∙ f2(y).
При решении дифференциальных уравнений с разделяющимися переменными полезно придерживаться следующей схемы:
- разделить переменные (т.е. в одной части уравнения должно быть выражение, содержащее только переменную х, в другой – переменную у);
- найти интегралы от обеих частей уравнения, найти частное решение уравнения;
- найти частное решение, удовлетворяющее начальным условиям (если они заданы).
Пример. Найти общее решение дифференциального уравнения: ydy + xdx = 0
Сначала разделим переменные, т.е. запишем уравнение в виде
ydy = -xdx,
затем найдем интегралы от обеих частей уравнения:
∫ ydy = -∫xdx,
получим 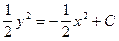
Пример. Найти общее решение дифференциального уравнения: 2уу′ = 1-3х2.
Заменим у′ = 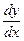 и умножим обе части уравнения на dx.
и умножим обе части уравнения на dx.
Получим: 2уdy = (1-3х2)dx,
Затем найдем интегралы от обеих частей:
2∫ уdy = ∫(1-3х2)dx,
у2 = х - х3+С.
Пример. Найти частное решение дифференциального уравнения (решить задачу Коши для заданных начальных условий): (1+x2)dy – 2x(y+3)dx = 0, если у = -1 при х = 0.
Сначала найдем общее решение. Разделим переменные (для этого выражение (– 2x(y+3)dx) перенесем в правую часть и разделим обе части уравнения на (1+x2)(y+3)).
Получим: 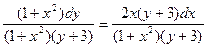 ,
,
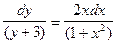 ,
,
найдем интегралы от обеих частей:
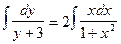
Вычислим отдельно каждый интеграл.
1. 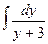 . Введем новую переменную t = у+3, тогда dt = (у+3)′∙ dу = dу, т.е. dt = dу. Подставим новую переменную в интеграл:
. Введем новую переменную t = у+3, тогда dt = (у+3)′∙ dу = dу, т.е. dt = dу. Подставим новую переменную в интеграл:
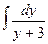 =
=  = ln
= ln  +C = ln
+C = ln 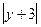 +C
+C
2. 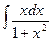 . Введем новую переменную t = 1+x2 , тогда dt = (1+x2)′∙ dx = 2xdx, откуда dx =
. Введем новую переменную t = 1+x2 , тогда dt = (1+x2)′∙ dx = 2xdx, откуда dx = 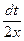 . Подставим новую переменную в интеграл:
. Подставим новую переменную в интеграл:
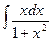 =
= 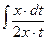 =
= 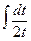 =
= 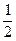 ln
ln 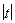 +C =
+C = 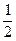 ln
ln 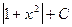
Найдем общее решение данного уравнения:
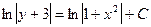
Для нахождения частного решения подставим в общее решение вместо х и у заданные начальные значения: 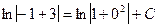 ,
,
найдем С: С = ln 2,
подставим в общее решение получившееся значение C:
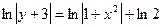
Пример. Найти общее решение дифференциального уравнения: 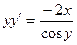
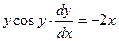
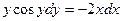
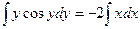
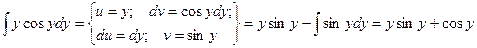

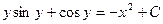
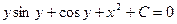 -
-
это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Пример. Найти решение дифференциального уравнения 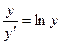 при условии у(2)= 1.
при условии у(2)= 1.
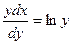
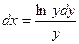
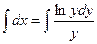
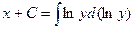
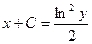
при у(2) = 1 получаем 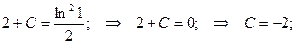
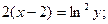 или
или 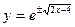 - частное решение;
- частное решение;
Пример. Решить уравнение 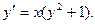
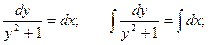
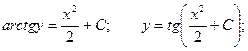
Пример. Решить уравнение 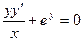 при условии у(1) = 0.
при условии у(1) = 0.
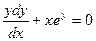
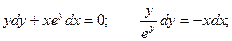
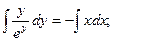
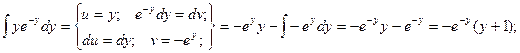
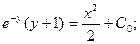
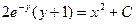
Если у(1) = 0, то 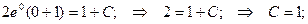
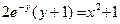 .
.
Пример. Решить уравнение 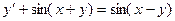 .
.
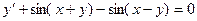
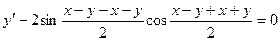
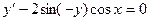
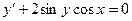
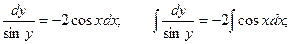
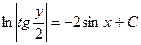
Пример. Решить уравнение 
Преобразуем заданное уравнение:
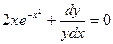
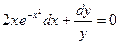
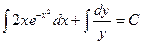
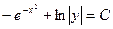
Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.
Дата добавления: 2020-06-09; просмотров: 913;











