Табличные значения производных основных функций
1. (un)' = n × un-1 × u' (n Î R)
2. (au)' = au × lna× u'
3. (eu)' = eu × u'
4.(loga u)' = 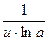 × u'
× u'
5. (ln u)' = 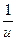 × u'
× u'
6. (sin u)' = cos u × u'
7. (cos u)' = - sin u× u'
8. (tg u)' = 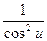 × u'
× u'
9. (ctg u)' = - 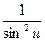 × u'
× u'
10. (arcsin u)' = 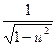 × u'
× u'
11. (arccos u)' = - 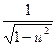 × u'
× u'
12. (arctg u)' = 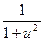 × u'
× u'
13. (arcctg u)' = - 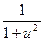 × u'
× u'
Пример. Найти производную функции у = х4 + 2х2 – 1
Для вычисления данной производной воспользуемся 1 табличным значением:
у′ = 4х4-1 + 2∙2х = 4х3 +4х
Пример. Найти производную функции у = 12х ∙ (х2 – 8)
Для вычисления производной воспользуемся сначала 3 правилом дифференцирования (u = 12x, v = х2 – 8), затем 1 табличным значением:
у′ = (12х)′ ∙ (х2 – 8) + 12х ∙ (х2 – 8)′ = 12 ∙ (х - 8) + 12х ∙2х = 12х – 96 + 24х2
Пример. Найти производную функции у = е3-4х
Данная функция является сложной, ее производная находится по 5 правилу дифференцирования. Обозначим u = 3 - 4х, тогда у = еu. Далее воспользовавшись 3 табличным значением производной, получим:
у′ = (eu)' = eu × u' = е3-4х ∙ (3 - 4х)′ = е3-4х ∙ (-4) = - 4 е3-4х
Пример. Вычислить производную функции: у = 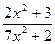
Данная производная вычисляется по 4 правилу дифференцирования (u=2x2+3, v=7x2+2):
у′ = 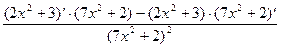 =
= 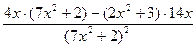 =
=
= 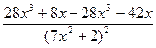 = -
= - 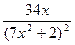
Пример. Вычислить производную функции: у = (5х2+3х-7)6
Данная функция является сложной. Обозначим u = 5х2+3х-7, получим функцию у = u6, для нахождения производной которой воспользуемся 1 табличным значением:
у′ = 6u5 = 6∙(5х2+3х-7)5 ∙ (5х2+3х-7)′ = 6∙(5х2+3х-7)5 ∙ (10x+3)
Пример. Вычислить производную функции: у = 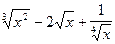
Для нахождения данной производной сначала преобразуем заданную функцию: у =  . Далее воспользуемся 1 табличным значением:
. Далее воспользуемся 1 табличным значением:
у′ = 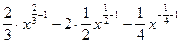 =
= 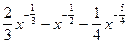 =
= 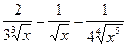
Дата добавления: 2020-06-09; просмотров: 825;











