Глава 6. Фазовые переходы

Агрегатные состояния и фазы. Уравнение Клапейрона-Клаузиуса

1. Агрегатные состояния вещества (от латинского aggrego – присоединяю) – это состояние одного и того же вещества в различных интервалах температур и давлений. Их 3: твёрдое, жидкое, газообразное.

Все простые химические вещества (элементы) в зависимости от температуры и давления могут находиться в любом из 3-х агрегатных состояний. В каждом температурном диапазоне реализуются разные комбинации (рис.91).

	Твердое (основное) + газообразное + жидкое (метастабильное)	Жидкое (основное) + газообразное	Газообразное (основное) + жидкое (метастабильное)

0 Т_пл Т_кипТ, К

Рис.91

Здесь Т_пл и Т_кип – температуры плавления и кипения вещества при данном постоянном давлении. При температуре выше критической Т_кр реализуется только одно газообразное агрегатное состояние.

2. Фаза (от греческого phasis – появление) – это широкое понятие. Фазой называют макроскопическую физически однородную часть вещества, отделённую от остальных частей системы границами раздела. Фаза может быть извлечена из системы механически. Могут быть однофазные, двухфазные и многофазные системы (рис.92).

На рис.92-а в системе одна газообразная фаза – пары воды. На рис.92-б – две фазы – жидкая (вода) и газообразная (пар). В третьей системе 92-в три фазы: газообразная (пар), жидкая (вода), твёрдая (лёд). Поскольку число возможных фаз у воды исчерпано, то дальнейший рост числа фаз в системе может происходить лишь за счет привлечения других веществ. На рис.92-г в системе 4 фазы: одна газообразная (пар), две жидкие (вода и капля ртути), одна твердая (лед). На рис.92-д показана 5-фазная система: одна газообразная (пар), две жидких (вода и ртуть), две твердых (лед и железо).

В одной системе могут быть сколько угодно твердых и жидких фаз, но только одна газообразная. Дело в том, что газы растворяются друг в друге неограниченно.

Если все фазы системы имеют одну и ту же температуру, то говорят, что система находится в тепловом равновесии.

3. Фазовый переход – это переход вещества в системе из одного фазового состояния в другое. Различают фазовые переходы 1-го рода (ФП-1) и 2-го рода (ФП-2).

ФП-1 сопровождаются скачкообразным изменением внутренней энергии или других связанных с ней величин – плотности, теплоёмкости. Все ФП-1 происходят при определённых температуре и давлении и сопровождаются поглощением либо выделением энергии.

ФП-2 не связаны с выделением или поглощением тела. Они сопровождаются скачкообразными изменениями одной или нескольких из следующих 3-х величин: а. Теплоёмкости C = dU/dT; б. Коэффициента теплового расширения a = (1/V)×( dV/dT)_p; в. Изотермического коэффициента сжимаемости вещества c = (1/V)×( dV/dp)_T.

К фазовым переходам 2-го рода, относятся, например, переход ферромагнетика (Fe, Ni, Co, сплавы, керамики) в парамагнитное состояние, превращение сегнетоэлектриков (BaTiO₃, KNaC₄H₄O₆×2H₂O, LiNiO, … всего несколько сотен) в неполяризованные диэлектрики и др.. Температура Т_С , при которой происходит ФП-2, называется точкой Кюри.

4. Фазовые переходы 1-го рода. К ним относятся все изменения агрегатного состояния вещества, то есть переходы: твёрдое состояние ↔ жидкое состояние, жидкость↔газ, твёрдое состояние↔газообразное состояние.

Переход из твёрдого состояния в жидкость называют плавлением, из жидкого в газообразное – испарением. Переход из твёрдого состояния в газообразное называют сублимацией(от лат. Sublimo - возношу) или возгонкой. Все перечисленные здесь переходы происходят с поглощением тепла. Обратные переходы сопровождаются выделением тепла. Переход в твёрдое состояние из жидкого или газообразного называют кристаллизацией, переход в жидкое из газообразного – конденсацией.

ФП-1 твёрдое тело ↔ жидкость характеризуется при определённом давлении температурной точкой плавления-кристаллизации Т_пл = Т_крист, молярной Λ и удельной λ теплотой плавления-кристаллизации.

Переход жидкость↔газ при определённом давлении характеризуется точкой кипения-росы Т_кип = Т_росы , молярной Â и удельной r теплотой испарения-конденсации.

Переход твёрдое тело-газ не имеет фиксированной температурной точки фазового перехода. Но при определённой температуре он характеризуется молярной D и удельной d теплотой возгонки-кристаллизации.

При фазовых переходах первого рода скачком изменяется внутренняя энергия вещества U (рис.93) и его теплоёмкость C_p (рис.94).Как видно из рис.93, график внутренней энергии U, построенный для 1 моля воды H₂O, в точках фазового перехода первого рода испытывает разрыв. В точке плавления Т_пл внутренняя энергия увеличивается на теплоту плавления, а в точке кипения – на теплоту испарения. Поскольку при плавлении и испарении скачком меняется и теплоёмкость (рис.94), то на графике U(T) на рис.93 скачком меняется также и угол наклона соответствующих участков кривой.

При переходах 1-го рода новая фаза не возникает сразу во всём объёме. Сначала образуются зародыши новой фазы, которые затем растут и распространяются на весь объём.

5. Уравнение Клапейрона-Клаузиуса является теоретической основой для прогнозирования поведения систем в фазовых переходах 1-го рода.

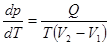. Б. Клапейрон, 1834, Р. Клаузиус, 1851 (23.1)

Здесь p – давление, T – температура, при которых происходит фазовый переход, Q – теплота фазового перехода, V₁ и V₂ – начальный и конечный объём вещества.

Рассмотрим вывод этого уравнения методом циклов на примере фазового перехода испарение - конденсация. Проведём мысленно цикл Карно с некоторым количеством вещества n так, чтобы в процессе цикла вещество проходило через разные фазовые состояния.

Состояние 1. Пусть в цилиндре под поршнем при температуре T и под давлением p находится n молей жидкости, объём которых в исходном жидком состоянии V₁ (рис.95).

Проведём изотермическое расширение системы при T = const. Это возможно лишь при условии, что жидкость будет испаряться. Чтобы температура оставалась постоянной, к жидкости нужно подводить тепло. Когда жидкость получит количество теплоты Q, равное теплоте испарения при температуре T, вся жидкость перейдет в газообразное состояние 2 с параметрами p, T, V₂ (рис.96).

Состояние 2. Из состояния 2 будем адиабатно расширять пар так, чтобы объем увеличился на величину dV. В конце расширения объем системы стал V₂+dV. Одновременно понижаются температура и давление, так что в конце адиабатного расширения система переходит в состояние 3 с параметрами p - dp, T - dT, V₂ + dV (рис.97).

Состояние 3. При температуре T - dT изотермически сжимаем пар при постоянном давлении p - dp. Чтобы поддержать постоянство температуры, нужно отводить тепло от системы. Когда количество отведенного тепла будет равным теплоте конденсации Q - dQ при температуре T - dT, весь пар сконденсируется в жидкость с параметрами T - dT, p-dp, V₁+dV. Система переходит в состояние 4 (рис.98).

Состояние 4. Чтобы вернуть систему в исходное состояние и замкнуть цикл, адиабатно сожмем жидкость на величину объема dV. В результате объем жидкости уменьшится до первоначальной величины V₁, а температура и давление повысится до величин T и p.

Найдем КПД цикла. 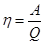. (23.2)

В системе координат p, V график цикла имеет форму бесконечно тонкого горизонтального четырехугольника (рис.99). Адиабаты 2®3 и 4®1, строго говоря, разные. В процессе 2®3 расширяется газ, а в процессе 4®1 сжимается жидкость. Однако поскольку четырехугольник бесконечно тонкий, разница в работах dA_2®3 и dA_4®1 есть величина 2-го порядка малости. Это позволяет считать работу цикла равной алгебраической сумме работ изотермических

процессов. dA = A_1®2+ A_3®4= p(V₂– V₁)+(p – dp)(V₁– V₂)=(V₂– V₁)dp. (23.3)

Теперь КПД идеального цикла Карно можно представить двумя способам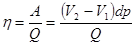и:

и 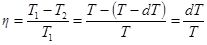(23.4)

Приравняв правые части этих выражений, получим 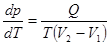. (23.5)

Примерно так это уравнение получил в 1834 г. Бенуа Клапейрон, а в 1851 г. Рудольф Клаузиус распространил его на все фазовые переходы 1-го рода.

Если в правой части уравнения разделить числитель и знаменатель на массу вещества m, то получаем уравнение в удельных величинах. 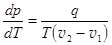. (23.6)

Здесь q – удельная теплота фазового перехода, v₁ и v₂ – удельные объемы вещества.