Тепловые свойства кристаллов
1. Тепловое расширение. Как показывает опыт, все тела при нагревании расширяются. Приращение dl линейного размера твердых тел пропорционально длине тела l и приращению температуры dT. dl = aldT. (21.1)
Здесь a – коэффициент линейного расширения твердого тела. Он зависит от материала и в общем случае несколько растет с температурой. Но если температурный интервал не превышает 150-200 K, коэффициент a в большинстве случаев в пределах этого интервала можно считать постоянным. Приращение длины тогда находится интегрированием от T0 до T и от l0 до l. 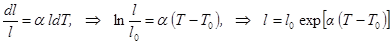 . (21.2)
. (21.2)
| Таблица 21 | |||
| Вещество | a, 10-6 K-1 | Вещество | a, 10-6 K-1 |
| Алюминий | Лед (-10°С) | ||
| Сталь | Медь | ||
| Инвар | Молибден | ||
| Кварц | 0,4 | Стекло | 0,008 |
| Кирпич | 0,9 | Фарфор | 0,003 |
Здесь l0 – длина тела при начальной температуре T0. Значения a известных в природе тел не превышают 10-4 K-1 (см. таблицу 21). Даже на температурном интервале в 1000 K, практически перекрывающем всю область существования веществ в твердом состоянии, показатель экспоненты aDT < 0,1. Это позволяет разложить экспоненту в ряд Тейлора по формуле 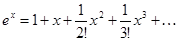 (21.3)
(21.3)
Ограничившись двумя членами ряда, получаем: 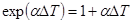 . (21.4)
. (21.4)
Тогда l = l0(1 + aDT). (21.5)
В формулу входит разность температур DT, поэтому не имеет значения, какой шкалой пользоваться – Цельсия или Кельвина. На практике чаще пользуются шкалой Цельсия. Если начальную длину l0 тела взять при начальной температуре 0°С, то l = l0(1 + at). (21.6)
Объем твердых тел при нагревании также растет линейно с температурой.
V = V0(1 + b t), где b = 3a. (21.7)
2. Классическая теория теплоемкости твердых тел. Кристаллическое твердое тело представляет собой совокупность атомов или молекул, находящихся в узлах кристаллической решетки и совершающих хаотическое колебательное движение. Поэтому кристалл можно рассматривать как систему осцилляторов. Подводимое к телу тепло идет на увеличение энергии колебания осцилляторов, складывающейся из кинетической и потенциальной.
Определим внутреннюю энергию твердого тела, полагая, что осцилляторы подчиняются законам ньютоновой механики. В этом случае каждый узел может колебаться в трех взаимно перпендикулярных направлениях. Полагаем осцилляторы гармоническими с непрерывно изменяющейся энергией.
Экстраполируя гипотезу Больцмана о равномерном распределении энергии по степеням свободы на кристаллы, получаем среднюю тепловую энергию одного узла.
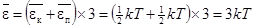 . (21.8)
. (21.8)
Внутренняя тепловая энергия твердого кристалла равна 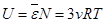 . (21.9)
. (21.9)
Изохорная теплоемкость твердого кристалла 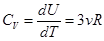 , CV=3R. (21.10)
, CV=3R. (21.10)
Итак, молярная теплоемкость всех твердых кристаллических веществ есть величина одинаковая для всех веществ, не зависящая от температуры и равная 3R.
Этот вывод был установлен экспериментально в 1819 г. французами Пьером Дюлонгом и Алексисом Пти, и известен как закон Дюлонга и Пти.
На практике измеряется обычно изобарная теплоемкость Cp. У кристаллов величины Cp и CV отличаются незначительно (таблица 22.).
| Таблица 22 | ||
| Вещество | Cp, Дж|(моль×К) | Cp|3R |
| Алюминий | 24,3 | 0,97 |
| Ванадий | 24,4 | 0,98 |
| Вольфрам | 24,9 | 1,00 |
| Железо | 25,2 | 1,01 |
| Титан | 25,1 | 1,01 |
| Цинк | 25,0 | 1,00 |
3. Трудности классической теории теплоемкости твердых тел. Дальнейшие исследования теплоемкости твердых тел, выполненное после Дюлонга и Пти, показали:
 а. Молярная теплоемкость большинства твердых кристаллов при температурах 273 ÷373 K близка к 3R и почти не зависит от температуры. Исключения составляют алмаз C, бериллий Be, бор B, кремний Si. У них теплоемкость CV много меньше 3R. Но с ростом температуры она приближается к 3R.
а. Молярная теплоемкость большинства твердых кристаллов при температурах 273 ÷373 K близка к 3R и почти не зависит от температуры. Исключения составляют алмаз C, бериллий Be, бор B, кремний Si. У них теплоемкость CV много меньше 3R. Но с ростом температуры она приближается к 3R.
б. При низких температурах T ≤ 100 K теплоемкость всех кристаллов быстро убывает, стремясь к нулю при T → 0.
 в. С приближением температуры к абсолютному нулю теплоемкость CV кристаллов уменьшается пропорционально кубу температуры, CV ~ T 3 при 0 < T < 50 K (рис.85).
в. С приближением температуры к абсолютному нулю теплоемкость CV кристаллов уменьшается пропорционально кубу температуры, CV ~ T 3 при 0 < T < 50 K (рис.85).
Классическая теория теплоемкости проста и наглядна. В этом ее преимущество. Но она не может объяснить отступление от закона Дюлонга и Пти. Это удается сделать лишь в рамках квантовых представлений.
3. Квантовые осцилляторы. Формула Планка. В 1900 г. немец Макс Планк предположил, что энергия узлов в кристалле изменяется не непрерывно, как у макротел, а порциями величиной hv, где v – частота колебаний осциллятора, h – постоянная Планка, называемая квантом действия, h = 6,6×10-34 Дж×с.
Энергия колебательного движения каждого узла решетки вдоль одного направления может принимать, по Планку, дискретный ряд значений e = nhv, (21.11)
где n = 0, 1, 2, 3, … – целое положительное число.
Планк предположил, что осцилляторы, колеблющиеся в данном направлении, распределены по энергиям ε в соответствии с законом Больцмана. 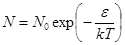 , (21.12)
, (21.12)
где N0 – число осцилляторов с нулевой энергией e = 0.
Вычислим среднюю энергию ансамбля таких квантовых осцилляторов, колеблющихся в одном направлении. 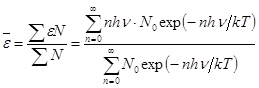 . (21.13)
. (21.13)
Введем обозначение hv| kT = x. Сократив числитель и знаменатель на N0 и вынеся за знак суммы в числителе множитель hv, получаем: 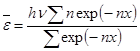 . (21.14)
. (21.14)
Это можно представить так: 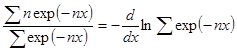 . (21.15)
. (21.15)
Сумма под знаком логарифма есть сумма членов бесконечной убывающей геометрической прогрессии. 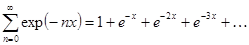 (21.16)
(21.16)
Она вычисляется по формуле 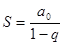 , (21.17)
, (21.17)
где a0 – первый член ряда, а q – знаменатель. Так как здесь a0 = 1, 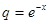 , то
, то
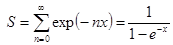 . Тогда (21.18)
. Тогда (21.18)
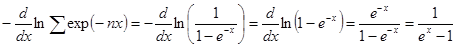 . (21.19)
. (21.19)
Итак, средняя энергия квантовых осцилляторов, колеблющихся вдоль одного направления, равна 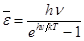 . Макс Планк, 1900. (21.20)
. Макс Планк, 1900. (21.20)
4. Теория теплоемкости твердых тел по Эйнштейну. В 1907 г. Альберт Эйнштейн предположил, что все узлы кристаллической решетки колеблются с одинаковой частотой ν. В этом случае, приняв, что средняя энергия узлов кристаллической решетки, колеблющихся вдоль одного направления, определяется формулой Планка, можно определить тепловую энергию кристалла 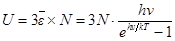 (21.21)
(21.21)
и его теплоемкость 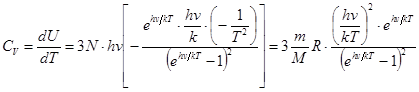 . (21.22)
. (21.22)
Исследуем эту формулу.
а. Пусть T велика, так что hn| kT << 1. Разложив exp(hn| kT ) в ряд по показателю hn| kT в точке нуль (формула 21.3) и ограничившись двумя первыми членами разложения, получаем для молярной теплоёмкости:
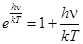 ,
, 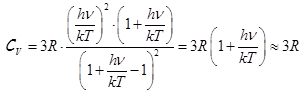 . (21.23)
. (21.23)
При высоких температурах, когда 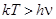 , теплоемкость по Эйнштейну совпадает с теплоемкостью Дюлонга и Пти.
, теплоемкость по Эйнштейну совпадает с теплоемкостью Дюлонга и Пти.
б. Пусть температура T мала, так что kT < hn. В этом случае exp(hn|kT ) >>1, разложение в ряд не годится. Но единицей в знаменателе (21.22) можно пренебречь.
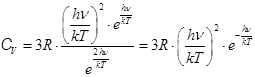 . (21.24)
. (21.24)
С понижением температуры T экспонента убывает быстрее, чем растет член (hn|kT)2, поэтому теплоемкость в целом уменьшается.
Теория теплоемкости по Эйнштейну не удовлетворяет эксперименту лишь в одном: CV → 0 при понижении температуры по экспоненте (формула 21.24), а на опыте – по кубической параболе.
5. Теория теплоемкости по Дебаю. В 1912 г. немец Петер Дебай развил теорию Эйнштейна, исходя из следующих предположений:
а. В твердом теле существует не одна частота, а целый набор частот колебаний – то есть спектр частот;
б. Этот спектр ограничен сверху некоторой определенной для каждого вещества максимальной частотой nmax;
в. Энергия каждого колебания частотой n равна hn. Этой энергии колебания hn в кристалле ставится в соответствие квантовая частица – фонон. В результате нагретый до определенной температуры кристалл рассматривается как однородное упругое тело с определенным спектром фононов.
| Таблица 23 | |||
| Вещество | qD, K | Вещество | qD, K |
| Алюминий | Алмаз | ||
| Вольфрам | Бериллий | ||
| Железо | Бор | ||
| Медь | Кремний | ||
| Цинк |
Теория Дебая лучше других удовлетворяет опыту. При kT > hn формула теплоемкости по Дебаю также переходит в закон Дюлонга и Пти. Критерием применимости классической теории является параметр, называемый характеристической дебаевской температурой qD = hnmax| k, где nmax – максимальная для данного вещества частота колебаний узлов, k – постоянная Больцмана.
Если температура тела больше дебаевской, T > qD, применима классическая теория, закон Дюлонга и Пти выполняется, CV = 3R. В таблице 23 приведены значения характеристической дебаевской температуры для некоторых веществ. Видно, что неподчинение алмаза, бериллия, бора и кремния закону Дюлонга и Пти объясняются тем, что у них очень высокая дебаевская температура.
В теории Дебая теплоемкость при температурах близких к абсолютному нулю, убывает по кубическому закону CV ~ T3. Эта теория наиболее точно определяет теплоемкость твердых кристаллических тел и их зависимость от температуры.
6. Теплопроводность твердых тел. Математическая теория теплопроводности, которую разработал Жан Фурье в 1822 г., была создана им как раз применительно к твердым телам. В основы ее лежала гипотеза теплорода. Тепловой поток рассматривался как поток жидкости (теплорода) в однородном пространстве твердого тела. Главным результатом теории Фурье было получение зависимости плотности теплового потока q от градиента температуры, 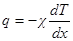 . Закон Фурье, 1822. (21.25)
. Закон Фурье, 1822. (21.25)
Здесь χ – коэффициент теплопроводности вещества.
С развитием атомно-молекулярных представлений о строении вещества стало ясно, что процесс теплопередачи в твердом теле есть направленный обмен энергиями колебательного движения между узлами кристаллической решетки.
Для построения теории теплопроводности плодотворной оказалась теория фотонов Дебая. В этом случае кристалл рассматривается как однородное тело, имеющее спектр собственных колебаний с частотами от 0 до nmax. Каждой частоте n ставится в соответствие некая фиктивная частица фонон с энергией hn, способная перемещаться в кристалле со скоростью звука 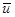 .
.
В результате твердое тело может трактоваться как сосуд с геометрией тела, наполненный газом из фононов. При не очень высоких температурах этот газ может считаться идеальным. А теплопроводность может быть представлена формулой (11.19), полученной в теории идеальных газов, 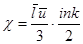 . (21.26)
. (21.26)
Здесь n – концентрация узлов в кристалле, 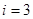 – число степеней свободы фононов,
– число степеней свободы фононов, 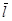 – их длина свободного пробега.
– их длина свободного пробега.
Фононная модель достаточно хорошо описывает теплопроводность диэлектриков.
| Таблица 24 | |||
| Вещество | c, Вт|(м×К) | Вещество | c, вт|(м×К) |
| Диэлектрики | Проводники | ||
| Бетон | 2,2 | Алюминий | |
| Гипс | 1,3 | Вольфрам | |
| Гранит | 3,4 | Золото | |
| Кирпич | 0,8 | Медь | |
| Мрамор | 3,5 | Серебро | |
| Слюда | 0,6 | Цинк |
В металлах коэффициент теплопроводности много больше, чем в диэлектриках (таблица 24). Это можно объяснить тем, что помимо колебаний узлов решетки в передаче тепла в металлах участвуют еще и электроны проводимости. Внутренняя тепловая энергия в металлах распределена между фононным и электронным газами.
С ростом температуры теплопроводность всех твердых тел уменьшается.
Твердые полимеры
1. Твердые полимеры – это вещества, релятивная молекулярная масса которых на 3-6 порядков больше массы атома водорода. Природные твердые полимеры-белки, целлюлоза, каучуки – являются важнейшей частью животного и растительного мира. В последнее столетие в народном хозяйстве исключительно широко стали применяться синтетические полимеры-смолы, пластмассы, ткани, органические стекла и др. В основе замечательных свойств твердых полимеров лежат химический состав и структура макромолекул.
2. Получение синтетических твердых полимеров, их называют часто высокомолекулярными веществами (ВМВ), осуществляется двумя основными методами – полимеризацией и поликонденсацией.
Молекулы низкомолекулярных веществ (НМВ), образующих полимер, называют мономерами. Число молекул мономера в макромолекуле называют степенью полимеризации и обозначают n. Число n в некоторых полимерах может достигать нескольких тысяч.
а. Полимеризация– это безотходная химическая реакция соединения главными валентностями молекул мономера с образованием молекул полимера того же элементного состава, как и исходное вещество. В качестве примера рассмотрим образование молекул полиэтилена и поливинилхлорида. 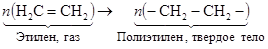 . (22.1)
. (22.1)
Реакция полимеризации полиэтилена идет при температуре t = 200°С и под давлением 2000 атмосфер без всяких катализаторов. Получающийся полиэтилен высокого давления не содержит вредных химических веществ и может использоваться для изготовления пищевой посуды. Степень полимеризации полиэтилена высокого давления n » 1600.
Использование реакторов высокого давления удорожает производство полиэтилена. Если применять катализатор триэтилалюминий с добавкой хлорида титана - 4TiCl4, то реакция идет при атмосферном давлении. Получающийся полиэтилен низкого давления имеет степень полимеризации n » 14000 и может применяться в изделиях, не связанных с пищевой промышленностью из-за содержащихся в нем вредных остатков катализатора.
Поливинилхлорид получается полимеризацией винилхлорида.
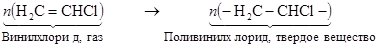 (22.2)
(22.2)
Поливинилхлорид – прекрасный диэлектрик, стойкий к действию кислот и щелочей. Широко используется для изготовления труб и сосудов в химической промышленности. Степень полимеризации n » 1500.
б. Поликонденсация – это реакция образования полимеров из мономеров с отщеплением воды, спиртов и других НMВ. Например, образование капрона.
n[NH2 - (CH2)5 - CO - OH] → n[NH - (CH2)5 - CO -] + nH2O
Степень поликонденсации может достигать здесь 1000 и более.
 3. Конформации. Свойства ВМВ зависят не только от химического состава, но также от размеров и формы макромолекул. Существуют три типа форм макромолекул: линейная, плоская, пространственная. Подавляющее большинство природных и искусственных ВМВ имеют линейные макромолекулы, напоминающие зигзаг, в углах которого находятся атомы углерода, ковалентные связи которых расположены под углом 109°28'. Длина таких линейных молекул достигает нескольких микрометров. Например, полиэтилен – 3 мкм, каучук – 0,8 мкм. Поперечник линейных макромолекул около 0,75 нм. Это позволяет изготовлять из таких ВМВ нити.
3. Конформации. Свойства ВМВ зависят не только от химического состава, но также от размеров и формы макромолекул. Существуют три типа форм макромолекул: линейная, плоская, пространственная. Подавляющее большинство природных и искусственных ВМВ имеют линейные макромолекулы, напоминающие зигзаг, в углах которого находятся атомы углерода, ковалентные связи которых расположены под углом 109°28'. Длина таких линейных молекул достигает нескольких микрометров. Например, полиэтилен – 3 мкм, каучук – 0,8 мкм. Поперечник линейных макромолекул около 0,75 нм. Это позволяет изготовлять из таких ВМВ нити.
Линейные макромолекулы могут изгибаться в пространстве. При этом каждое звено в цепи может изменять свое положение не произвольно, а лишь двигаясь по поверхности конуса с валентным углом при вершине (рис.86).
Различные формы одной и той же молекулы называют конформациями. Чем больше звеньев в молекуле, тем больше конформаций она может иметь. Среди всех возможных конформаций есть энергетически более выгодные, они соответствуют минимуму потенциальной энергии e min, и энергетически менее выгодные, соответствующие максимуму энергии e max.
Для перехода молекулы из положения с минимальным значением энергии e min в положение с e max требуется затрата энергии e = e max - e min, которая характеризует потенциальный барьер вращения. Чем больше e, тем более устойчива молекула к механическим деформациям. В пересчете на 1 моль потенциальный барьер вращения E = eNA »104 Дж|моль. Это почти на порядок больше тепловой энергии RT , приходящейся на колебательную степень свободы при нормальной температуре T = 273 K.
Теоретические оценки показывают, что вероятность изменения положения звена пропорциональна величине exp(-E| RT). С ростом температуры степень свободы вращения звеньев возрастает. При RT << E (холодно) звенья совершают, в основном, колебательные движения относительно положения равновесия. Цепь более вытянута и жесткая. При RT » (0,2 ÷ 0,3)E молекулы приобретают достаточную гибкость, полимерное изделие легко поддается деформациям кручения и изгиба.
4. Термомеханические свойства полимеров. Имеется много низкомолекулярных веществ, в которых при охлаждении настолько быстро возрастает вязкость, что перемещение и вращение молекул затормаживается еще до образования кристаллической решетки. По механическим свойствам эти вещества подобны твердым телам, а по молекулярной структуре - жидкостям. Такие вещества называют аморфными. К ним относятся минеральные стекла природного (вулканическое стекло-обсидиан) и искусственного (оконное, посудное, оптическое) происхождения, смолы, битумы, янтарь, глицерин и др.
Температура, при которой вязкость аморфных тел приближается к вязкости кристаллов, называется температурой стеклования Tc. Состояние аморфного тела при T < Tc называют стеклообразным, а при T > Tc жидким. При охлаждении полимеров их вязкость также резко увеличивается. Поэтому кристаллизация полимеров при охлаждении, наблюдается гораздо реже, чем переход в застеклованное состояние.
| Таблица 25 | |
| Полимер | Tc, °С |
| Натуральный каучук | - 73 |
| Поливинилацетат | + 28 |
| Нейлон | + 47 |
| Нитроцеллюлоза | + 53 |
| Оргстекло | + 57÷68 |
| Полистирол | + 81 |
| Этилцеллюлоза | + 43 |
| Бутадиеновый каучук | - 40 |
В таблице 25 приведены значения температуры стеклования Tc для некоторых наиболее известных полимеров. Температура стеклования является одним из важнейших параметров, определяющих практическое использование полимеров. Например, резиновые шины нельзя эксплуатировать в морозы при температуре, ниже температуры стеклования каучука, на основе которого изготовлена резина. Нейлоновую ткань нельзя гладить утюгом с температурой выше температуры стеклования и так далее.
 С повышением температуры выше Tc макромолекулы восстанавливают гибкость, сохраняя в то же время межмолекулярные связи. В этом состоянии полимер обладает высокоэластичными свойствами, он легко деформируется и способен к значительным удлинениям.
С повышением температуры выше Tc макромолекулы восстанавливают гибкость, сохраняя в то же время межмолекулярные связи. В этом состоянии полимер обладает высокоэластичными свойствами, он легко деформируется и способен к значительным удлинениям.
С дальнейшим ростом T после некоторого значения Tт, называемого температурой текучести, межмолекулярные связи макромолекул настолько ослабляются, что получают возможность взаимного смещения. Это состояние полимера называют вязкотекучим.
Таким образом, аморфные ВМВ, в отличие от аморфных НМВ, имеют не два (твердое и жидкое), а три физические состояния – стеклообразное, высокоэластичное и вязкотекучее. Это не агрегатные состояния.
На рис.87 показана зависимость относительной деформации Dl| l полиизобутилена от температуры T. Кривая 1 соответствует числу звеньев в молекуле n = 1200, а кривая 2 – числу звеньев n = 60000. Из рисунка видно, что температура текучести Tт, соответствующая резкому изгибу кривой вверх, тем больше, чем больше звеньев в молекуле.
Опыт показывает, что ширина интервала DT = Tт - Tc и число звеньев в молекуле n связаны соотношением 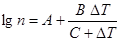 , (22.4)
, (22.4)
Где А, В и С – константы. Для полиизобутилена, например, A = 1,35, B = 6,7, C = 263 K. Измерив интервал Tт - Tc и вычислив число звеньев n полимера, можно оценить его релятивную молекулярную массу Mr.
 Температура стеклования Tc определяется величиной потенциального барьера вращения молекул и почти не зависит от длины макромолекул. Температура текучести Tт, напротив, соответствует началу взаимного движения макромолекулярных цепей. Она тем больше, чем длиннее макромолекула.
Температура стеклования Tc определяется величиной потенциального барьера вращения молекул и почти не зависит от длины макромолекул. Температура текучести Tт, напротив, соответствует началу взаимного движения макромолекулярных цепей. Она тем больше, чем длиннее макромолекула.
5. Кристаллизация полимеров. В твердых полимерах существуют два типа структур: свернутые молекулы (глобулы) и пачки вытянутых цепей (фибриллярные пучки).
Если фибриллярные пучки образованы гибкими молекулами регулярного строения, то существующая в цепях упорядоченность структуры может приводить в некоторых областях полимера к кристаллической упорядоченности. Образование таких кристаллов можно рассматривать как возникновение в аморфном полимере новой кристаллической фазы, обладающей границами раздела и поверхностным натяжением. Эти области называют кристаллитами (рис.88).
Не все полимеры могут кристаллизоваться. Аморфными, например, остаются эбонит, синтетические каучуки. Лучше кристаллизуются гибкие макромолекулы простого строения - полиэтилен, политетрафторэтилен (тефлон), нейлон. Эти ВМВ образуют кристаллиты уже при комнатной температуре. Например, полиэтилен при 20°С закристаллизован на 50 - 70%.
6. Полимеры – неньютоновые жидкости. В идеально упругих твердых телах относительная деформация сдвига g = x| l пропорциональна приложенному касательному напряжению τ, то есть 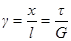 . Роберт Гук, 1660 (22.5)
. Роберт Гук, 1660 (22.5)
 Здесь G – модуль сдвига. В жидкостях G = 0. В простых жидкостях – вода, спирт, глицерин и др. – напряжению пропорциональна не относительная деформация сдвига γ, а скорость изменения деформации сдвига
Здесь G – модуль сдвига. В жидкостях G = 0. В простых жидкостях – вода, спирт, глицерин и др. – напряжению пропорциональна не относительная деформация сдвига γ, а скорость изменения деформации сдвига 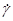 . Это следует из закона Ньютона для вязких жидкостей (рис.89).
. Это следует из закона Ньютона для вязких жидкостей (рис.89). 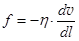 (22.6)
(22.6)
Здесь f – сила вязкого трения, действующая по касательной на единичную площадь параллельно слоям текущей жидкости, h - вязкость жидкости, dv| dl – градиент скорости.
Преобразуем формулу закона Ньютона.
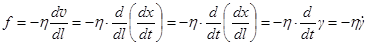 . (22.7)
. (22.7)
Так как f = t - касательному напряжению, то формулу закона Ньютона (22.7) можно еще переписать так: 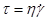 . Ньютонова жидкость. (22.8)
. Ньютонова жидкость. (22.8)
Для сравнения: 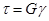 . Твердое тело. Закон Гука. (22.9)
. Твердое тело. Закон Гука. (22.9)
В формуле (22.8) знак «минус» опущен, то есть формула написана не для тормозящего жидкость напряжения, а для движущего.
 Многие растворы полимеров отличаются тем, что у них скорость течения
Многие растворы полимеров отличаются тем, что у них скорость течения 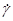 растёт быстрее, чем приложенное напряжение τ. В результате с ростом напряжения сдвига τ измеряемый коэффициент вязкости h падает.
растёт быстрее, чем приложенное напряжение τ. В результате с ростом напряжения сдвига τ измеряемый коэффициент вязкости h падает.
На рис.90 прямая 1 соответствует ньютоновой жидкости. Течение начинается при сколь угодно малых напряжениях, скорость течения строго пропорциональна напряжению (при вязком безвихревом течении).
Кривая 2 соответствует неньютоновой жидкости. Скорость течения растет быстрее напряжения. В процессе течения свойства неньютоновой жидкости меняются.
Кривая 3 соответствует системам, которые до некоторого минимального напряжения tmin ведут себя как твердое тело. Начиная с этого минимального напряжения tmin система начинает течь и ведет себя как неньютоновая жидкость с переменной вязкостью вплоть до некоторого напряжения tН. Начиная с этого момента, система ведет себя как ньютоновая жидкость с постоянной вязкостью. Это так называемые пластичные системы: глинистые растворы, фармацевтические пасты и кремы, схватывающийся гипс.
8. Эластомеры. Из рис.86 видно, что в цепной молекуле достаточно уже нескольких десятков звеньев, чтобы расположение конца цепи относительно начала имело случайный характер. В вытянутой цепи между концом и началом возможно только одно расстояние rmax. В свернутой цепи это расстояние r может изменяться от 0 до rmax, и оно постоянно меняется вследствие теплового движения. Теория и опыт показывают, что средний квадрат расстояния 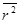 пропорционален числу звеньев n в цепи,
пропорционален числу звеньев n в цепи, 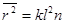 . (22.10)
. (22.10)
Здесь l – длина цепи, k – коэффициент, зависящий от валентного угла.
При растяжении клубка цепь переходит в менее вероятное состояние и при снятии напряжения самопроизвольно возвращается к более свернутой конформации. Большое различие между линейными размерами свернутого клубка и длиной вытянутой цепи делает возможными большие обратимые деформации. Такие высокоэластичные полимеры называют эластомерами. К ним относятся различные каучуки и изготовленные на их основе резины.
Относительная упругая деформация в кристаллах не превышает нескольких процентов, тогда как каучук можно растягивать в 10 раз. Модуль упругости металлов составляет около 100 ÷ 200 ГПа, у резины он меньше 1 ГПа, а у некоторых каучуков всего лишь 1 МПа, что в 200 000 раз меньше модуля упругости стали.
Эти различия объясняются тем, что при упругих деформациях кристаллов изменяются валентные расстояния между атомами, что связано со значительным изменением внутренней энергии. В эластомерах же большие удлинения происходят без изменения валентных расстояний при постоянстве внутренней энергии (вплоть до трехкратных удлинений). Высокоэластические свойства каучука являются результатом теплового движения молекул. Деформация каучука напоминает деформацию идеального газа
Так, при адиабатическом сжатии газ нагревается. Каучук также нагревается при быстром растяжении. Это так называемый термоэластический эффект. А вот кристаллы при растяжении охлаждаются.
Кинетическая теория упругой деформации эластомеров имеет выход в биологию живых организмов, так как оказалось, что белковые молекулы мышц обладают каучукоподобными свойствами.
Дата добавления: 2020-05-20; просмотров: 976;











