В консервативных системах

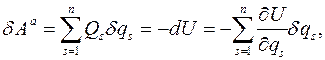
Поэтому обобщенные силы равны

,

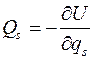где 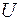есть, по определению, потенциальная энергия системы. В этом случае в положениях равновесия 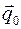потенциальная энергия системы имеет экстремум:

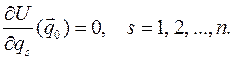
Дифференциальный принцип механики на перемещениях, не совместимых со связями.

На элементарных перемещениях системы 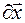, несовместимых со связями, дифференциальный принцип механики применяется тогда, когда движение системы известно (найдено), и необходимо найти силы контактного взаимодействия (силы реакций связей).

Для каждого тела системы с номером s , s = 1, 2, … , N , элементарные перемещения 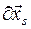, несовместимые со связями, могут быть двух типов. Это либо поступательное перемещение (трансляция) 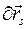, либо поворот 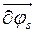. Поэтому для системы N тел принцип можно записать так:

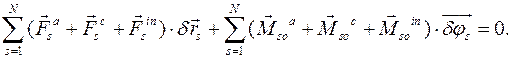
Здесь для каждого тела 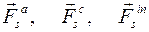есть главные векторы активных сил, сил контактного взаимодействия и сил инерций, а 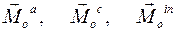есть главные моменты соответствующих сил относительно полюса трансляции .

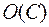Принцип применяют либо ко всем телам системы, либо к любому количеству тел (одному телу) системы.

Так как 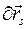, 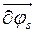не удовлетворяют уравнениям связей, то они произвольны и независимы. Тогда:

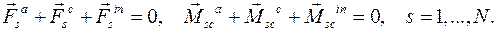
Для одного твердого тела (N = 1) из определения главного вектора сил инерций 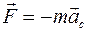и определения главного момента сил инерций 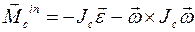, из дифференциального принципа следуют дифференциальные уравнения движения абсолютно твердого тела, причем второе уравнение записывают в подвижном базисе:

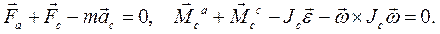
Таким образом, из дифференциального принципа механики следуют дифференциальные уравнения движения твердого тела в виде теоремы о движении центра масс и теоремы об изменении момента импульса тела относительно центра масс.Последняя теорема записана в подвижном базисе.

Для системы 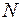твердых тел в аналогичных уравнениях движения присутствуют внешние силы системы тел.

Консервативная система. Вычислениепотенциальной энергии потенциальных сил.

Сила тяжести 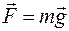. В декартовых осях Oxyz , где ось Oy направлена по вертикали,

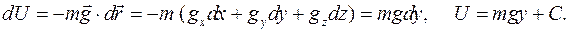
Если принять, что U(O) = 0, то константа С = 0, и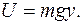

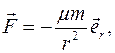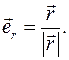Центральная сила гравитационного притяжения где В сферических координатах имеем:

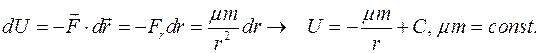
Если принять, что U(∞) = 0, то 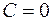и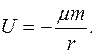

Сила упругой пружины 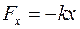, где 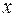есть удлинение (сжатие) пружины. Коэффициент 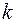- жесткость пружины. Сила не зависит от направления пружины, а зависит только от ее удлинения (сжатия), поэтому

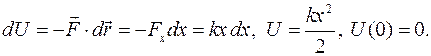
Здесь x есть удлинение (сжатие) пружины в текущем положении, а dx есть элементарное удлинение пружины при ее растяжении.