Сложение угловых скоростей и угловых ускорений в сложном движении твердого тела.

Представим абсолютное движение твердого тела как два движения.

Введем неподвижную, абсолютную систему координат 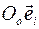. Тогда абсолютное движение тела определяется движением полюса О и матрицей абсолютного вращения .

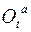Введем подвижную систему координат 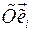, по отношению которой относительное движение тела определяется относительным движением 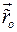полюса 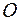и матрицей относительного вращения 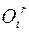, а переносное движение – движением полюса подвижной системы координат 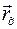и матрицей ее вращения .

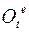Наконец, для индивидуализации точек тела, как и раньше, зададим в теле систему координат 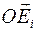, жестко связанную с телом.

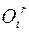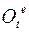Исследуем только вращательные части относительного и переносного вращений, заданные матрицами и соответственно, игнорируя при этом все поступательные движения. Это значит, что начала всех систем координат совпадают, и точка О есть неподвижная точка тела. Тогда абсолютное вращение тела есть композиция двух последовательных аффинных преобразований с ортогональными матрицами. Поэтому матрица абсолютного вращения 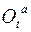определяется как произведение матриц 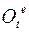и 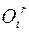, а абсолютное движение любой точки тела

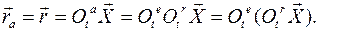
Абсолютная скорость любой точки тела 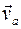есть для сферического движения

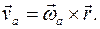
Здесь вектор 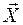последовательно перезаписывается сначала в подвижном базисе ( 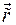), а затем в неподвижном ( ).

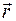С другой стороны, представляя движение тела как сложное, можем вычислить скорость точки 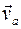так:

Таким образом,

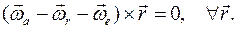
Значит, выражение в скобках равно нулю.

Здесь 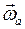, , 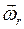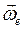есть угловые скорости абсолютного, относительного и переносного вращений соответственно.

В результате получаем теорему о сложении векторов угловых скоростей относительного 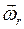и переносного 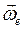вращений:

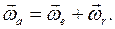
Дифференцируя по времени это выражение, докажем теорему о сложении угловых ускорений твердого тела в сложном движении:

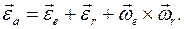
Доказательство:

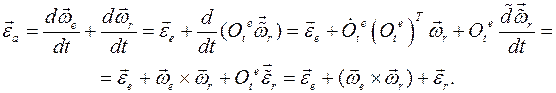
Здесь 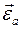, , 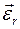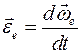и 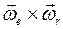есть абсолютное, относительное и добавочное угловые ускорения.