Свободные оси вращения. Гироскоп

1. Свободные оси вращения. Рассмотрим два случая вращения твердого стержня относительно оси, проходящей через центр масс.

Если раскрутить стержень относительно оси OO и предоставить его самому себе, то есть освободить ось вращения из подшипников, то в случае рис.71-а ориентация оси свободного вращения относительно стержня будет изменяться, поскольку стержень под действием пары центробежных сил инерции будет разворачиваться в горизонтальную плоскость. В случае рис.71-б момент пары центробежных сил равен нулю, поэтому раскрученный стержень будет продолжать вращаться вокруг оси ОО и после ее освобождения.

Ось вращения, положение которой в пространстве сохраняется без действия каких-либо сил извне, называется свободной осью вращающегося тела. Следовательно, ось, перпендикулярная стержню и проходящая через его центр масс, есть свободная ось вращения стержня.

У любого твердого тела есть три взаимно перпендикулярные свободные оси вращения, пересекающиеся в центре масс. Положение свободных осей для однородных тел совпадает с положением их геометрических осей симметрии (рис.72).

У параллелепипеда все три оси фиксированы. У цилиндра фиксирована только одна ось, совпадающая с геометрической осью. У шара все три оси не фиксированы.

Свободные оси вращения называются также главными осями инерции. При свободном вращении тел вокруг главных осей инерции устойчивы лишь вращения вокруг тех осей, которым соответствуют максимальное и минимальное значения момента инерции. Если же на тело действуют внешние силы, то устойчивым оказывается вращение лишь вокруг той главной оси, которой соответствует максимальный момент инерции.

2. Гироскоп(от греческого gyreuo – вращаюсь и skopeo – вижу) – быстро вращающееся вокруг оси симметрии однородное тело вращения, ось которого может изменять положение в пространстве.

При изучении движения гироскопа считаем, что:

а. Центр масс гироскопа совпадает с его неподвижной точкой O. Такой гироскоп называется уравновешенным.

б. Угловая скорость w вращения гироскопа вокруг оси много больше угловой скорости Wперемещения оси в пространстве, то есть w >> W.

в. Вектор момента импульса гироскопа L совпадает с вектором угловой скорости w, поскольку гироскоп вращается вокруг главной оси инерции.

Пусть на ось гироскопа действует сила F в течение времени Dt. По второму закону динамики для вращательного движения 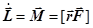, так что изменение момента импульса гироскопа за это время 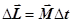, (26.1)

где r – радиус-вектор, проведенный из неподвижной точки O в точку действия силы (рис.73).

Изменение момента импульса гироскопа можно рассматривать как поворот оси гироскопа на угол 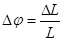с угловой скоростью 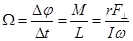. (26.2)

Здесь 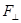– нормальная к оси гироскопа составляющая действующей на него силы.

Под действием силы F, приложенной к оси гироскопа, ось поворачивается не в направлении действия силы, а в направлении момента силы M относительно неподвижной точки O. В любой момент времени скорость поворота оси гироскопа пропорциональна по величине моменту силы, а при постоянном плече силы – пропорциональна самой силе. Таким образом, движение оси гироскопа безинерционно. Это единственный случай безинерционного движения в механике.

Движение оси гироскопа под действием внешней силы называют вынужденной прецессией гироскопа (от латинского praecessio – движение впереди).

3. Ударное действие на ось гироскопа. Определим угловое смещение оси гироскопа в результате кратковременного действия силы на ось, то есть удара. Пусть в течение малого времени dt на ось гироскопа на расстоянии r от центра О действует сила F. Под действием импульса этой силы Fdt ось поворачивается (рис.74) в направлении создаваемого ею импульса момента силы Mdt на некоторый угол

dq = Wdt=(rF/Iw)dt. (26.3)

Если точка приложения силы не изменяется, то r = const и при интегрировании получаем. q = 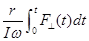. (26.4)

Интеграл в каждом случае зависит от вида функции 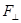(t). В обычных условиях угловая скорость вращения гироскопа очень велика, поэтому числитель чаще всего много меньше знаменателя, и потому угол q – малая величина. Быстро вращающийся гироскоп обладает устойчивостью по отношению к удару – тем большей, чем больше его момент импульса.

4. Интересно, что сила, под действием которой ось гироскопа прецессирует, не совершает работы. Это происходит потому, что точка гироскопа, к которой приложена сила, в любой момент смещается в направлении, перпендикулярном направлению действия силы. Поэтому скалярное произведение силы на вектор малого перемещения всегда равно нулю.

Силы в таком проявлении называются гироскопическими. Так, всегда гироскопической является сила Лоренца, действующая на электрически заряженную частицу со стороны магнитного поля, в котором она движется.

5. Условие равновесия ТТ.Чтобы ТТ находилось в равновесии, необходимо, чтобы сумма внешних сил и сумма моментов внешних сил были равны нулю:

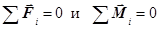. (26.5)

Различают 4 вида равновесия: устойчивое, неустойчивое, седлообразное и безразличное.

а. Положение равновесия ТТ является устойчивым, если при небольших отклонениях от равновесия на тело начинают действовать силы, стремящиеся вернуть его в положения равновесия.

На рисунке 75 показаны ситуации устойчивого равновесия тел в поле силы тяжести. Силы тяжести – массовые силы, поэтому равнодействующая сил тяжести, действующих на точечные элементы ТТ, приложена к центру масс. В таких ситуациях центр масс называют центром тяжести.

Устойчивому положению равновесия соответствует минимум потенциальной энергии тела.

б. Если при небольших отклонениях от положения равновесия на тело начинают действовать силы в направлении от равновесия, то положение равновесия является неустойчивым. Неустойчивому положению равновесия соответствует относительный максимум потенциальной энергии тела (рис.76).

в. Седлообразным является такое равновесие, когда при движении по одной степени свободы равновесие тела устойчивое, а при движении по другой степени свободы – неустойчивое. В ситуации, показанной на рисунке 77, положение тела по отношению к координате x является устойчивым, а по отношению к координате y – неустойчивым.

г. Если при отклонении тела от положения равновесия не возникает никаких сил, стремящихся сместить тело в том или ином направлении, то положение равновесия называется безразличным. Например, шар в поле силы тяжести на эквипотенциальной поверхности, твердое тело, подвешенное в точке центра масс (в точке центра тяжести) (рис.78).

В тех случаях, когда тело опирается на опору, то чем больше площадь опоры и чем ниже центр тяжести, тем устойчивее равновесие тела (рис.79).