Способы решения задач на движение осесимметричных ТТ

В качестве примера возьмем скатывание с наклонной плоскости сплошного цилиндра массы m. Скатывание происходит без скольжения и без потерь энергии. Найдем ускорение центра масс.

1. Способ 1. Составляем уравнение моментов относительно мгновенной оси вращения A:

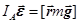. (25.1)

Здесь I_A – момент инерции тела относительно оси A, 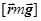– момент внешних сил (рис.68).

На тело действует сила тяжести mg, приложенная к центру масс тела к точке C, ее момент относительно точки A есть 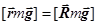, где R – радиус диска. Сила реакции опоры слагается из нормальной силы реакции N и касательной силы трения F_тр. Обе силы реакции приложены к точке A и их момент равен нулю. В проекции на мгновенную ось вращения получаем: 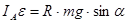. Отсюда линейное ускорение центра масс

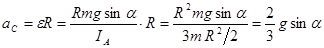. (25.2)

Тело (точка C − его центр масс) движется равноускоренно. Линейная скорость любой точки тела 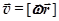, где r – радиус-вектор от мгновенной оси вращения А до данной точки.

Из системы уравнений 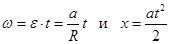находим .

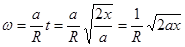Отсюда, линейная скорость любой точки тела есть 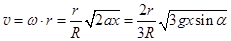. (25.3)

2. Способ 2. Составляем уравнение моментов относительно оси, проходящей через центр масс тела точку C, 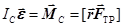. (25.4)

Моменты сил тяжести и нормальной реакции равны нулю (рис.69). Но сила F_тр неизвестна. Поэтому для решения задачи нужно еще одно уравнение. Воспользуемся теоремой о движении центра масс. В проекции на ось Х уравнение движения центра масс имеет вид: ma_C = mgsina – F_тр. (25.5)

Итак, получили систему из двух уравнений, которую разрешим относительно a_C.

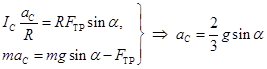. (25.6)

3. Способ 3. Если скатывание происходит без потерь механической энергии, то для решения задачи можно использовать закон сохранения механической энергии (рис.70).

Полагаем в точке х = 0 E_П = 0 и E_К = 0. Тогда в любой точке х полная механическая энергия равна: 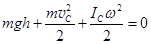. (25.7)

Так как h = – xsina, то .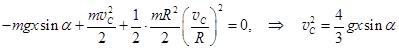

Скорость пропорциональна корню квадратному из пути, 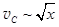. Но это присуще равноускоренному движению. Следовательно, 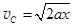. Отсюда 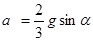. (25.8)

В том, что к процессу, в котором действуют силы трения, применяется закон сохранения механической энергии, нет противоречия. Здесь силы трения приложены к точкам тела, лежащим на мгновенной оси вращения, и потому работа сил трения равна нулю. Если же есть проскальзывание, то работа сил трения не равна нулю, и закон сохранения механической энергии не выполняется.

4. Итак, уравнение моментов, составленное относительно мгновенной оси вращения тела, полностью описывает движение тела. В этом случае достаточно одного уравнения.

Если уравнение моментов составляется для центра масс, не лежащего в общем случае на мгновенной оси вращения, то необходимо еще одно уравнение – теорема о движении центра масс.