Гидродинамика идеальной несжимаемой жидкости.

1. Идеальная жидкость. В тех случаях, когда роль сил трения в текущих жидкостях сравнительно невелика, ими можно пренебречь. Такая модель жидкости, в которой отсутствует трение, называется идеальной жидкостью. Законы динамики идеальной жидкости наиболее просты.

2. Линии тока. Для описания идеальной жидкости применяется понятие линий тока. Это линии, в каждой точке которых вектор скорости движения частиц жидкости направлен по касательной. По сути – это траектории движущихся частиц (рис.94).

Непрерывное множество линий тока образуют трубку тока (рис.95).

3. Уравнение неразрывности струи. Из условия постоянства объема жидкости следует уравнение неразрывности струи. В любой момент времени объемы жидкости, протекающие в трубке тока через сечения в разных ее частях, одинаковы. Отсюда v₁s₁ = v₂s₂ =¼= const. (29.1)

Это уравнение неразрывности. Здесь v – линейная скорость движения частиц жидкости.

4. Уравнение Бернулли. Если внешние силы, вызывающие движение жидкости, не зависят от времени, то через некоторое время после начала движения в жидкости установится вполне определенное распределение скоростей. Такое движение жидкости называется установившимся (стационарным).

В 1738 г. Даниило Бернулли вывел соотношение между величинами, характеризующими стационарное движение идеальной несжимаемой жидкости.

p+ 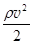+ rgh = const. Уравнение Бернулли (29.2)

Уравнение Бернулли выражает закон сохранения энергии применительно к идеальной жидкости. Здесь 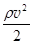– кинетическая энергия единичного объема жидкости, rgh – потенциальная энергия единичного объема жидкости в поле силы тяжести, p - внутрижидкостное давление.

Размерности энергии (единицы объема) и давления совпадают. Поэтому члены уравнения Бернулли называют еще так: p - статический напор, rgh - гидравлический напор, 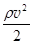- динамический напор. Если записать уравнение для двух сечений s₁ и s₂ , трубки тока (рис.96) p₁+ 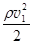+ rgh₁ = p₂+ 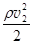+ rgh₂, то легко видеть, что чем меньше сечение трубки s, тем больше скорость течения жидкости, тем больше динамический напор и тем меньше статический напор − давление на стенки.

5. Формула Торричелли. Воспользуемся уравнением Бернулли для определения скорости вытекания струи из узкого отверстия в стенке широкого сосуда (рис.97).

Пусть из сосуда с жидкостью, площадь зеркала которой s₁, вытекает из отверстия в стенке, площадь которого s₂ << s₁ струя. Запишем уравнение Бернулли для сечений s₁ и s₂.

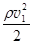p₁+ + rgh₁ = p₂+ 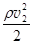+ rgh₂.

Статическое давление в жидкости в сечениях s₁ и s₂ одинаковое (атмосферное), поэтому p₁ = p₂.Начало координат выбрано так, чтобы h₂ = 0. Отсюда

rgh₁ = 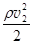и v₂ = 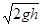. Формула Торричелли, 1641г. (29.3)

Идеальная жидкость вытекает из сосуда с высотой уровня над отверстием h с такой же скоростью, с какой она свободно падала бы с этой же высоты.

6. Течение жидкости в горизонтальной трубе переменного сечения. Выясним, как изменяется давление в разных точках трубы переменного сечения (рис.98). Так как h₁ = h₂ , то уравнение Бернулли для сечений s₁ и s₂ принимает вид: p₁ + 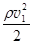= p₂ + 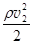. Из уравнения неразрывности v₁s₁ = v₂s₂. Тогда v₂ = v₁s₁/s₂, и перепад давления составляет p₁ - p₂ = 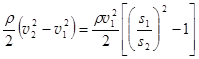. (29.4)

Чем меньше сечение трубы, тем больше скорость течения жидкости, тем меньше статический напор. В узких местах трубы статический напор может сделаться меньше, чем давление снаружи трубы. В этом случае, если в стенке трубы сделать отверстие, то труба будет действовать как насос. Так действуют, например, водоструйный насос, пульверизатор, карбюратор.

7. Обтекание несимметричных тел. Подъемная сила. Рассмотрим обтекание полуцилиндра. Поскольку жидкость несжимаема, то при обтекании полуцилиндра частицам жидкости, находящимся на линиях тока 1 и 2 , приходится проходить разный путь и, следовательно, двигаться с разными скоростями (рис.99).

Запишем уравнение Бернулли для линий тока 1 и 2: p₁ + 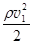= p₂+ 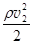. Здесь v₁çv₂ = pRç2R, откуда v₁ = pv₂ç2. Между нижней и верхней поверхностями полуцилиндра возникает перепад давлений

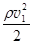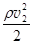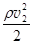
p₂ - p₁ = - = 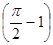. (29.5)

На плоскую поверхность давление больше, чем на выпуклую. В результате перепада давлений возникает сила, которую называют подъемной (рис.100). F = DP×s (29.6)

В общем случае подъемная сила возникает всегда, когда обтекаемое жидкостью тело несимметрично. Эта сила в значительной мере делает возможным горизонтальный полет летательных машин тяжелее воздуха. Наряду с подъемной силой здесь используется также подъемная составляющая динамического напора, обусловленная положительным углом атаки крыла (рис.101).