Теорема Гюйгенса-Штейнера. Физический маятник.

<19 20 212223 24 25 >

1. Теорема Гюйгенса-Штейнера. Найдем связь между моментами инерции тела относительно двух параллельных осей (рис.62).

Пусть O и А – оси, перпендикулярные плоскости рисунка и параллельные между собой, причем точка O – центр масс тела. Найдем момент инерции тела относительно оси А, параллельной оси, проходящей через центр масс O, и находящейся от нее на расстоянии a.

В общем случае 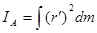. Но 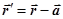. Отсюда

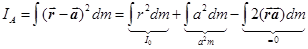. (23.1)

Последнее слагаемое равно нулю. Действительно, вынеся из-под знака постоянный вектор a, получаем: 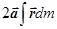. Но 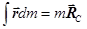, где m – масса тела, R_C – радиус-вектор центра масс. Поскольку точка отсчета помещена в центр масс тела, то R_C= 0, поэтому все слагаемое обращается в нуль. Итак, 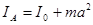. Теорема Гюйгенса-Штейнера (23.2)

Момент инерции тела относительно произвольной оси A равен моменту инерции I₀относительно параллельной ей оси, проходящей через центр масс, сложенному с величиной ma², где m – масса тела, a – расстояние между осями.

Христиан Гюйгенс (1629–1695) – нидерландский механик, физик и математик, создатель волновой теории света. В 1655 г. открыл планету Титан, спутник Сатурна, открыл кольцо Сатурна. В 1657 г. изобрел первые маятниковые часы. В 1673 г. нашел решение задачи об определении центра качаний физического маятника. Определил формулу центростремительного ускорения.

Пример 23.1 Момент инерции сплошного цилиндра относительно образующей (рис.63).

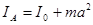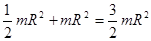= . (23.3)

Пример 23.2 Момент инерции шара относительно касательной(рис.64).

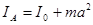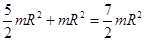= . (23.4)

3. Физический маятник – это твердое тело, способное качаться вокруг неподвижной оси в однородном поле силы тяжести.

Составим уравнение движения маятника (рис.65). В точке С находится центр масс маятника. 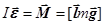. (23.5)

Спроектируем уравнение на ось OZ цилиндрической системы координат. (Ось OZ на рис.65 совпадает с осью вращения). Положительное направление оси OZ должно быть согласовано с положительным направлением отсчета угла j по правилу правого винта. 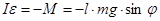. (23.6)

Так как 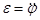, то, ограничившись малыми углами j, когда sinj≃j, получаем: 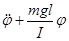=0. (23.7)

Это уравнение гармонических колебаний. Период колебаний маятника составляет T=2 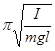. (23.8)

Выражение I/ml имеет размерность длины и называется приведенной длиной физического маятника, 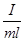= l_пр. Период колебаний маятника T = 2 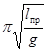. (23.9), (23.10)

Период колебаний физического маятника, выраженный через приведенную длину, такой же, как период колебаний математического маятника с длиной нити, равной l_пр.

Приведенная длина l_пр= 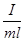> l. Действительно, если выразить момент инерции по теореме Гюйгенса-Штейнера, 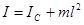, где I_C – момент инерции маятника относительно параллельной оси, проходящей через центр масс, то l_пр= 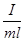= = 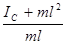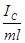+l > l.

4. Теорема Гюйгенса. Вычислим период колебаний маятника, подвешенного в точке O', лежащей в конце приведенной длины (рис.66). T'=2 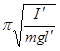, где l' = l_пр– l. Здесь I' – момент инерции маятника относительно точки O'. Так как I' = I_C+ m(l_пр – l)², то 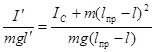. Поскольку l_пр– l = 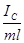, то 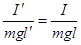. Тогда T' = 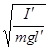= = 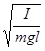T. (23.11)

Следовательно, как показал в 1673 г. Х.Гюйгенс, период колебаний тела, подвешенного в точке O', такой же, как и подвешенного в точке O, отстоящей от точки O на расстоянии приведенной длины. Это теорема Гюйгенса.

Точку O' называют центром качаний. Это точка, в которую должна, собраться масса физического маятника, чтобы его период качаний остался без изменений. Теорема Гюйгенса используется в лабораторной работе для измерения ускорения свободного падения с помощью оборотного маятника (Метод Бесселя).