Принцип относительности Галилея

1. Инерциальные системы отсчета (ИСО). Все системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. Закон инерции можно сформулировать ещё так: всегда можно найти такую систему отсчета, в которой тело, на которое не действуют силы, движется прямолинейно и равномерно или покоится.

2. Принцип относительности Галилея. Выясним, изменится ли выражение второго закона Ньютона, описывающего движение материальной точки М в инерциальной системе отсчета К, если это движение рассматривать относительно другой системы К ¢, движущейся относительно ИСО К прямолинейно и равномерно (рис.20).

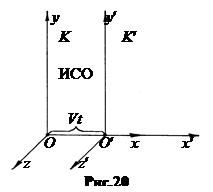В системе К: 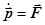. Так как v << c, то . Спроектировав на оси, получаем . (8.1)

Чтобы выяснить, как изменится формула второго закона Ньютона, надо установить, как изменяются входящие в формулу величины при переходе из одной системы отсчёта в другую.

Из трёх величин – массы, силы и ускорения – одна величина – масса – сохраняется с очевидностью (закон сохранения массы в классической механике). Сила взаимодействия между объектами определяется расстоянием между объектами или относительной скоростью их движения. Следовательно, сила есть функция отрезков и разностей скоростей взаимодействующих тел. Если воспользоваться преобразованиями Галилея (3.11, 3.12), то можно убедиться, что длины отрезков и разности скоростей не меняются при переходе от одной системы отсчета к другой. Говорят, отрезки и разности скоростей инвариантны относительно преобразований Галилея. А это значит, что и сила, являющаяся функцией инвариантных величин, также инвариантна. Итак, масса тел и сила взаимодействия между телами не зависят от выбора системы отсчета.

Чтобы установить, как изменяется ускорение тел при переходе из одной системы отсчета в другую, нужно дважды продифференцировать преобразование Галилея для координат по времени t = t ¢.

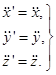а так как V = const, то (8.2)

Итак, ускорение тел как их масса и сила взаимодействия между ними, инвариантно по отношению к преобразованиям Галилея. Но если все величины, входящие во второй закон Ньютона, не меняются при переходе из одной системы отсчета в другую, то это значит, что не меняется проявление этого закона, он сохраняет свою форму.

Отсюда следует, что все системы отсчета, движущиеся прямолинейно и равномерно относительно инерциальной, являются также инерциальными. Законы Ньютона в них проявляются одинаково. В этом суть принципа относительности Галилея.

Все механические процессы во всех ИСО протекают одинаково. Значит, никакими механическими экспериментами нельзя установить, движется данная ИСО равномерно и прямолинейно, или покоится. Следовательно, по характеру протекания механических процессов нельзя выделить из множества ИСО какую-то преимущественную. Все инерциальные системы отсчета механически равноправны.