Способ I. Способ 2.

Кинематика точки. Основные понятия

1. Кинематика (от греч. kinema – движение) - раздел механики, изучающий геометрию движения тел без учета причин движения. Кинематика использует понятия: пространство, время, тело отсчета, система координат, система отсчета, перемещение, траектория, скорость и ускорение.

2. Тело отсчета - это произвольно выбранное тело, относительно которого определяется положение точки и описывается её движение.

Для количественного описания положения и движения точки используется система координат (СК), жёстко связанная с телом отсчёта.

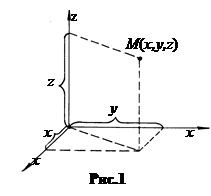
Прямоугольная (декартова) СК (рис.1).

Положение точки М определяется здесь с помощью трех чисел (x, y, z), имеющих размерность длины.

O

Название осей:

ОX – ось абсцисс,

ОУ – ось ординат,

OZ – ось аппликат.

Точка О - центр СК. Единичные векторы (единичные орты) i, j, k, задают направления положительного отсчёта по осям.

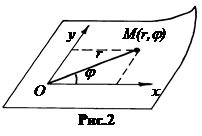Полярная СК применяется для исследования плоского движения точки (рис.2).

Одна координата, обычно обозначаемая буквами r или r – полярный радиус, другая, j - полярный угол. Точка О - полюс, OX - полярная ось.

Переход от полярной СК к декартовой осуществляется по формулам:

x = r×sinj , y = r×sinj. (3.1)

Выбор СК в общем случае произволен и делается так, чтобы описание движения точки было наиболее простым.

3. Система отсчёта –совокупность тела отсчёта, связанной с ним системы координат и часов. Не следует смешивать систему отсчета с системой координат. Если система координат – геометрический образ, то система отсчета, как правило, физическая реальность. Правда, в классической механике пространство и время не зависят друг от друга, поэтому смешивание этих понятий не приводит к количественным ошибкам в решениях задач, оно ограничивается лишь терминологической путаницей.

4. Траектория точки - это мысленный след от точки в пространстве. Траектория - непрерывная линия. Форма траектории зависит от выбора системы отсчета.

5. Кинематический закон движения точки - это уравнение, определяющее положение точки в пространстве в любой момент времени. Различают три способа написания кинематического закона движения (говорят, три способа задания движения): координатный, естественный, векторный. Рассмотрим их.

а. Координатный. Определяется тело отсчета, выбирается связанная с ним удобная для решения задачи система координат. Положение точки в пространстве определяется в любой момент времени тремя числами - координатами точки в выбранной СК. В декартовых координатах закон движения точки имеет вид: 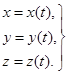(3.2)

Если из уравнений можно исключить время t, то получается уравнение траектории точки.

Пример 3.1

На плоскости: x = t, y = 4t² Þ y = 4x²

Если время t исключить из уравнений не удается, то форму траектории можно определить, подставляя в уравнения кинематического закона движения произвольные моменты времени t.

Пример 3.2 Таблица 3.1

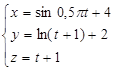
	t
x
y		2.7	3.1	3.4	3.6	3.8	3.9	4.1
z

Нанеся точки на график и соединив их линией, получаем графический образ траектории.

Продифференцировав закон движения точки по времени t, получаем проекции скорости на координатные оси.

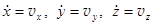(3.3)

После второго дифференцирования по t получаем проекции ускорения на оси.

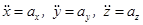. (3.4)

Умножив проекции скорости или ускорения на соответствующие единичные орты и сложив их, получаем выражения векторов скорости или ускорения.

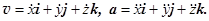(3.5)

Пример 3.3

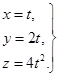
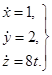
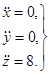
Закон движения Проекции скорости Проекции ускорения

Вектор скорости v = i + 2j + 8tk, ускорения a = 8k.

Закон движения представляет собой 3 независимых друг от друга уравнения. Это значит, что движение тел по одной координате не зависит от движения по другой. Этот факт был установлен Галилеем и назван им принципом независимости движений.

Пример3.4 Тело брошено под углом к горизонту a со скоростью v₀. Найти закон его движения.

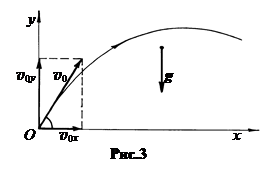
Выбираем координатный способ описания. Прямоугольную систему координат располагаем так, чтобы ось ОY была противоположна вектору ускорения свободного падения g. Тогда ось ОХ будет перпендикулярна ему. Начало CК помещаем в точку бросания (рис.3). При этих условиях движение тела вдоль оси ОY есть движение тела, брошенного вертикально вверх с начальной скоростью v_0y = v₀sina . Закон движения по оси ОY есть:

y = v_0yt – .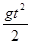

Вдоль оси ОХ тело движется равномерно со скоростью v_0x = v₀cosa

Закон движения по оси ОХ есть: x = v_0xt.

Итак: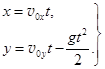

Задание: из закона движения тела, брошенного под углом к горизонту, найти уравнение траектории, проекции скорости и ускорения тела, векторы скорости и ускорения.

б. Естественный, или траекторный способ задания используется, когда известна траектория движения точки по отношению к выбранной системе отсчета. Этот способ удобен тем, что сводит описание движения к одномерному случаю. Из трех, в общем случае, уравнений остается одно.

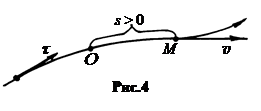На траектории, по которой движется точка М, выбирается точка О - начало отсчета, от которой отсчитывается смещение точки М вдоль траектории. Кроме того, выбирается положительное направление кривой. Оно задается единичным вектором касательной t (рис.4).

Скорость точки М всегда направлена по касательной к траектории. Проекция скорости v на траекторию положительна, если направление скорости совпадает с направлением единичного вектора касательной t, и отрицательна, если векторы v и t противоположны.

Закон движения имеет вид: s = s(t) (3.6)

Проекция скорости: 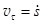. Вектор скорости: v = 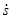t. Проекция ускорения 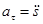(3.7)

Пример3.5 Закон движения по кривой есть: s = t² + 2cos4t.

Проекция скорости: 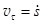= 4t - 8sin4t. Вектор скорости: v = (4t - 8sin4t)t.

Проекция ускорения: 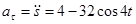. Вектор ускорения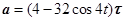

Естественный способ задания часто используется тогда, когда траектория жёстко задана. Например, точка на ободе маховика при его вращении движется только по окружности (в системе отсчета, связанной с механизмом, куда входит маховик), рельсовые транспортные средства движутся по путям и т.д.

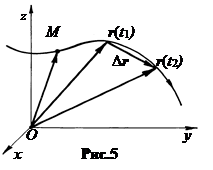
в. Векторный способ задания. Положение точки М по отношению к системе координат определяется вектором r, проведённым из центра СК в точку М. Такие векторы, проведенные из центра СК, называются радиусами-векторами (рис.5).

Траекторией точки М является в этом случае кривая, по которой движется конец радиуса-вектора r. Кривую, которую описывает конец радиуса-вектора r, называют ещё годографом радиуса-вектора.

Закон движения при векторном задании имеет вид:r = r(t). (3.8)

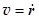Вектор скорости: . (3.9)

Вектор ускорения: 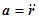. (3.10)

Не следует смешивать понятия "смещение" и "вектор перемещения" Термин "смещение" используется при естественном задании движения точки. Смещение s эквивалентно координате x точки М при движении вдоль выбранной оси координат.

Термин "вектор перемещения" используется при векторном задании. Вектор перемещения Dr есть вектор, проведенный из положения точки М в какой-то момент времени t₁, в положение точки в последующий момент времени t₂. Очевидно, Dr = r(t₂) - r(t₁). Проекции вектора перемещения на оси координат дают перемещения вдоль осей Dx = x₂ - x₁, Dy = y₂ - y₁, Dz = z₂ - z₁.

И естественный, и векторный способы задания движения точки сводятся к координатному.

6. Путь. В практике часто применяется понятие "пройденный телом путь", под которым понимается сумма смещений по траектории, взятых по абсолютной величине.

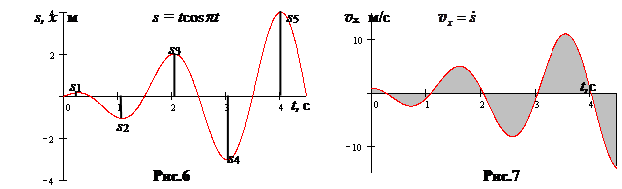При естественном задании путь удобно вычислять графически двумя способами.

Способ I. Способ 2.

Строится график смещения S (рис.6). Строится график проекции скорости (рис.7).

Путь есть сумма смещений, Путь есть сумма модулей площадей фигур

взятых по модулю S= 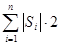. (на рисунке заштрихованы).

Перемещение по оси ОХ на рис.6 равно самой координате, т.к. движение началось из начала координат. Перемещение точки на рис.7 равно сумме площадей под графиком с учётом их знака.

7. Преобразования Галилея.При переходе от одной системы отсчета к другой координаты и скорости движения точки меняются.

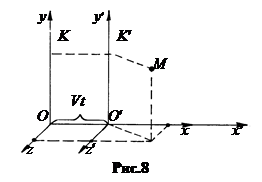Пусть есть две системы отсчёта К и К ¢. Выберем такую их взаимную ориентацию, чтобы скорость их относительного движения была направлена вдоль какой-либо оси, например, оси ОХ. На рис.8 оси ОХ и O¢X ¢ направлены вдоль одной прямой. Это упрощает поиски ответа на вопрос: как изменяются координаты и скорости точки при переходе от одной системы отсчета к другой.

Допустим, штрихованная система К ¢ движется поступательно вдоль оси O¢X ¢ относительно нештрихованной с постоянной скоростью V. Если координаты точки М в штрихованной системе есть x¢, y¢, z¢, то в нештрихованной их координаты есть:

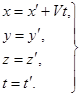Это преобразования Галилея для координат (3.11)

Время в обеих системах полагается независимым и одним и тем же.

Продифференцируем преобразования для координат по времени. Так как время в обеих системах одинаково, t = t¢, то

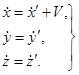Преобразования Галилея для скоростей (3.12)

Формулы преобразований Галилея справедливы в случае, когда скорость относительного движения тел отсчета постоянна по величине и по направлению, V= const.

Если умножить уравнения преобразований Галилея для скоростей на соответствующие единичные орты, которые в случае нашего выбора ориентации осей СК одинаковы, i = i¢, j = j¢, k = k¢,и сложив уравнения, то получаем закон сложения скоростей в векторном виде:

v_xi +v_yj +v_zk = v¢_xi¢ +v¢_yj¢ +v¢_zk¢+ V или v = v¢ + V.(3.13)

Это выражение справедливо при любой ориентации осей систем координат и при любой скорости их относительного движения (как постоянной, так и переменной).