Тригонометрическая форма комплексного числа

Понятие о комплексных числах. Алгебраическая, тригонометрическая, показательная формы записи комплексных чисел. Геометрическая интерпретация комплексных чисел. Действия над комплексными числами.

Понятие мнимой единицыДопустим, что существует такое число, квадрат которого равен – 1. Обозначим это число буквой i; тогда можно записать:

i² = – 1.

Число i будем называть мнимой. Из этого равенства находим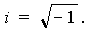

Введение мнимой единицы позволяет нам теперь извлекать корни квадратные из отрицательных чисел.

Например,

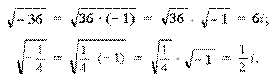
Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.

Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части.

Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей, т.е., если

a + bi = c +di, то a = c, b = d.

Геометрическая интерпретация комплексного числаКомплексное число z= a + bi можно изобразить точкой Z плоскости с координатами (a; b) (рис.1).

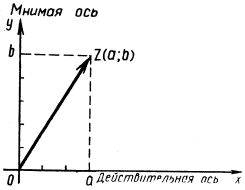
Рис.1

Для этого выберем на плоскости декартову прямоугольную систему координат. Действительные числа изображаются точками оси абсцисс, которую называют действительной (или вещественной) осью; чисто мнимые числа – точками оси ординат, которую будем называть мнимой осью.

Каждой точке плоскости с координатами (a; b) соответствует один и только один вектор с началом O(0; 0) и концом Z(a; b). Поэтому комплексное число z = a + bi можно изобразить в виде вектора с началом в точке O(0; 0) и концом в точке Z(a; b).

Пример 1. Изобразить на плоскости числа z₁ = 5; z₂ = – 3i; z₃ = 3 + 2i; z₄ = 5 – 2i; z₅ = – 3 + 2i; z₆ = – 1 – 5i.

Решение. Заданные числа изображены на рис. 2.

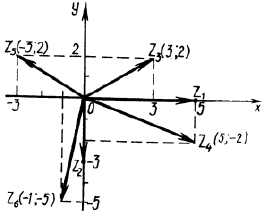Рис. 2

Действие над комплексными числамиa+bj и c+djв алгебраической форме

1) Правило сложения и вычитания комплексных чисел.

(a + bi) + (c + di) = (a + c) + (b + d)i.

Например:

+ =

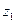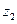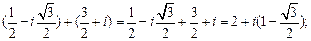
Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле:

(a + bi) – (c + di) = (a – c) + (b – d)i.

Например:

- =

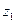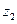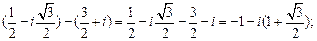
2) Правило умножения комплексных чисел.

(a + bi)(c + di) = (aс + bd) + (ad + bc)i.

Из определений 4 и 5 следует, что операции сложения, вычитания и умножения над комплексными числами осуществляются так, как будто мы выполняем операции над многочленами, однако с условием, что i2 = – 1.

Действительно: (a + bi)(c + di) = ac + adi + bdi2 = (ac – bd) + (ad + bc)i.

Например, * =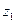

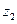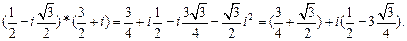
В частности, при умножении двух комплексных чисел a + bi и a – bi, называемых сопряженными комплексными числами, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части. Действительно:

(a + bi)(a – bi) = a² – abi + abi – b²i² = a² + b².

Произведение двух чисто мнимых чисел – действительное число.

Например: 5i•3i = 15i² = – 15.

3) Деление комплексного числа a + bi на комплексное число c + di определяется как операция обратная умножению и выполняется по формуле:

.

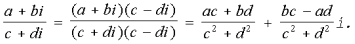Формула теряет смысл, если c + di = 0, так как тогда c² + d² = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.

Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.

Например,

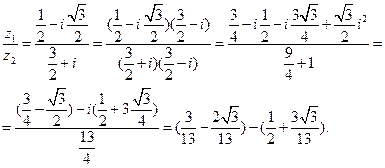
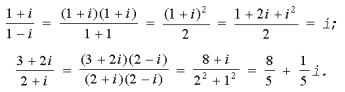
Тригонометрическая форма комплексного числа

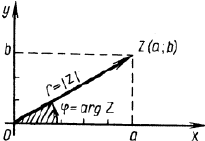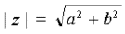Пусть комплексное число z = a + bi изображено в виде вектора с началом в точке O(0; 0) и концом Z(a; b) рис. 3 Определение 3. Модулем комплексного числа z = a + bi называется длина вектора , которую можно найти по формуле Обозначив модуль комплексного числа буквой r.

Рис. 3

Определение 4. Аргументом комплексного числа называется угол φ, который образует вектор с положительным направлением оси абсцисс. Величину угла φ можно найти с помощью формул: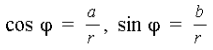

z = r (cos φ + i sin φ) называется тригонометрической формой комплексного числа.

Сформулируем правило перехода от алгебраической формы комплексного числа к тригонометрической.

1. Находят модуль комплексного числа r, для чего используют формулу

2. Для нахождения φ сначала определяют геометрически, в какой четверти находится точка z.

3. Составляют уравнения 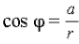и 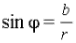и по решению одного из них находят угол φ.

4. Записывают комплексное число z в тригонометрической форме.