Потери в поршневых компрессорах.

Действительные рабочие процессы в холодильных компрессорах необратимы, сопровождаются объемными и энергетиче­скими потерями. Объемные потери уменьшают подачу и холодопроизводительность реального компрессора, а энергетические потери увеличивают подводимую мощность. Оценка эффективности работы действительного компрессора производит­ся путем сравнения его с идеальным компрессором.

Объемные потери.

Идеальный холодильный компрессор работает без потерь. У него нет вредного простран­ства, гидравлических сопротивлений во всасывающем и нагнета­тельном трактах, утечек пара хладагента из рабочей полости через неплотности. В нем отсутствуют трение и теплообмен между хлад­агентом и стенками рабочей полости (проточной части), а также трение между движущимися частями компрессора. . Поэтому в процессе всасывания давление в цилиндре равно давлению в испарителе, процесс сжа­тия осуществляется адиабатно (обратимо), а процесс нагнетания протекает при постоянном давлении в цилиндре, равном давлению в конденсаторе.

На рис. 2.17, а, в координатах V, р (объем, давление) представ­лена теоретическая индикаторная диаграмма поршневого идеаль­ного компрессора с адиабатным сжатием.

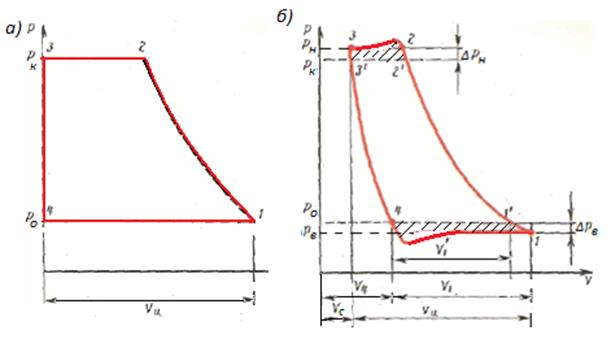
Рис. 2.17. Теоретическая (а) и действительная (б) индикаторные диаграммы поршневого холодильного компрессора.

Так как в компрессоре нет вредного пространства, индикаторная диаграмма примыкает к оси ординат. Тогда в начале всасывающего хода поршня (при V = 0) в цилиндре компрессора происходит мгновенное падение давления от давления нагнетания до давления всасывания (линия 3—4). Отсутствие гидравлических сопротивлений на стороне всасывания и во всасывающих клапанах компрессора, а также теплообмена хладагента со стенками цилиндра приводит к тому, что в про­цессе всасывания (линия 4—1) давление поступающего в цилиндр хладагента остается постоянным и равным давлению кипения в ис­парителе (p_B =p₀ = const). Отсутствие теплообмена и гидравлических сопротивлений на стороне нагнетания и в нагнетательных клапанах также ведет к постоянству давления в процессе нагнетания (линия 2—3) и равенству давлению в конденсаторе (p_н = p_K = const). Энергия к хлад­агенту подводится в процессе адиабатного сжатия (линия 1—2). Линия сжатия строится по уравнению pV^k = const (где k — показа­тель адиабаты).

Объемная теоретическая подача поршневого компрессора V_T-(м³/с) равна объему, описываемому поршнями компрессора в еди­ницу времени,

V =Vzn = 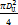szn, (2.1)

V_ц – рабочий объем цилиндра, м³; z – число работающих цилиндров; n – частота вращения коленчатого вала, с^-1; D_ц – диаметр цилиндра, м; s – ход поршня, м;

Теоретическая холодопроизводительность компрессора (кВт)

Q_т = m_тq₀ = V_тq_v, (2 2)

где q₀ – удельная массовая холодопроизводительность хладагента, кДж/кг; q_v – удельная объемная холодопроизводительность хладагента, q_v = q₀/v₁ .

Под холодопроизводительностью компрессора понимается холодопроизводительность холодильной машины, обеспечиваемая работой компрессора, т.е. количество теплоты, отводимое машиной от охлаждаемого объекта в единицу времени при заданных условиях.

Мощность, подводимая к идеальному поршневому компрессору, равна его внутренней , т.е. теоретической индикаторной мощности (кВт)

N_iТ = ml_Т (2 3)

где m – массовый расход хладагента, кг/с; l_Т – удельная теоретическая работа, затрачиваемая на сжатие 1 кг хладагента, кДж/кг.

При адиабатном сжатии удельная работа идеального компрессора равна

l_Т = 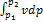= i₂ – i₁ = , (2 4)

и соответствует площади 1234 индикаторной диаграммы.

Массовый расход хладагента G_а будет определяться следующим выражением:

G_а = 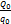, кг/с (2.5)

где Q₀ - заданная холодопроизводительностькомпрессора;

q₀ – удельная массовая холодопроизводительность холодильного агента.

Индикаторная диаграмма реального компрессора показана на рис . 2.17 .б

При работе реального компрессора поршень не подходит к крышке цилиндра (см. рис. 2.17 б). Между поршнем при его верхнем (крайнем) положении и крышкой цилиндра имеется зазор, который называется линейным вредным (мертвым) пространством. Для вертикальных и угловых компрессоров он равен 0,5 – 1,2 мм. Линейный зазор создается для того, чтобы во время работы исключить возможность удара поршня о крышку цилиндра при нагревании кривошипно-шатунного механизма. Относительный объем вредного пространства c, в который включают и объем выемок в клапанах, выражают в процентах от рабочего объема цилиндра (обычно 2 – 5%)

c = 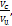(2.6)

где V_с – объем вредного пространства; V_ц – рабочий объем цилиндра.

Наличие вредного пространства приводит к значительным объем­ным потерям. Процесс выталкива­ния сжатых паров из цилиндра компрессора заканчивается в точ­ке 3, после чего при обратном дви­жении поршня расширяется сжатый пар, оставшийся во вредном про­странстве (линия 3—4). Всасыва­ние пара начинается только в со­стоянии, определяемом точкой 4. Часть цилиндра, измеряемую от­резком V_c1 , занимает расширенный пар. Объемные потери от расширения будут зави­сеть главным образом от объема вредного пространства V_c и отно­шения давлений р_к/р_о. При зна­чительном возрастании этого отно­шения компрессор может иметь даже нулевую подачу, когда пар, расширяющийся из вредного про­странства, займет весь объем ци­линдра.

При обратном политропном расширении (линия 3′ – 4) потерянный полезный объем V₄(см. рис. 2.17,б .) будет равен

V₄ = V_c 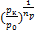, (2. 7)

где V_c – вредный объем цилиндра; p_к – давление конденсации; p₀ – давление кипения;

n_p – показатель политропы.

Уменьшение производительности действительного компрессора из-за расширения рабочего вещества, оставшегося во вредном пространстве оценивается объемным коэффициентом λ_с

λ_с = 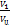(2. 8)

где V₁ – оставшийся полезный объем цилиндра

Учитывая, что V₁ можно определить как

V₁ = V_ц + V_c – V₄

c учетом выражений (2.6) и (2.7), объемный коэффициент примет вид

λ_с = 1 – c 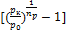(2. 9)

Из полученной зависимости видно, что с увеличением отношения p_к/p₀ объемный коэффициент уменьшается.

Коэффициент дросселированияλ_др учитывает уменьшение производительности из-за потерь давления во всасывающих клапанах (гидравлическим сопротивлением во всасывающей магистрали пренебрегаем). Всасывание пара и нагнетание происходит через самодействующие клапаны, которые открываются под действием разности давления пара хладагента, вследствие чего сжатие начинается при давлении более низком p_в , чем давление кипения p₀.

Рис. 2.17,б показывает, что давление, равное давлению кипения, при котором закроется всасывающий клапан, достигается в цилиндре в точке 1́́́ʹ после того, как поршень прошел часть хода от НМТ к ВМТ. Тогда коэффициент дросселирования

λ_др = 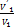(2. 10)

Значения коэффициента дросселирования зависят от конструкции всасывающих клапанов, рода хладагента и температурного режима компрессора. При движении хладагента через клапаны вследствие гидравлических сопротивлений возникают потери, которые могут достигать одной трети мощности, подводимой к валу компрессора. Уменьшить эти потери можно увеличением проходных сечений клапанов либо увеличением их количества. Для низкотемпературных холодильных машин с низким давлением всасывания значения коэффициента дросселирования лежат в пределах 0,95 – 0,98.

Объемная потеря от подогрева холодильного агентасвязана с тем, что в процессе всасывания рабочее вещество, соприкасаясь с горячими стенка­ми цилиндра, крышкой и поршнем, нагревается. При этом его удельный объем увеличивается и, хотя фактический объем всасываемого в цилиндр рабочего вещества остается неизменным, масса его уменьшается при неизменной объемной производитель­ности компрессора. Эта потеря производительности является скрытой и не может быть определена из индикаторной диаграмме. Объемная потеря от подогрева определяется коэффициен­том подогреваλ_ω. С увеличением отношения давлений λ_ω уменьшается. Также он меньше у бессальниковых компрессоров по сравнению с сальниковыми. Кроме перечисленных факторов, значительное влияние на λ_ω оказывает вид хладагента. Так, хладагенты с высоким показателем изоэнтропы (например, аммиак) имеют меньшие значения коэффициента подогрева из-за более высокой температуры нагнетания, а значит и большего нагрева деталей компрессора.

При ориентировочном определении коэффициента подогрева можно использовать эмпирическую формулу Левина

λ_ω = T₀/T_к (2.11)

где T₀ – температура кипения, К; T_к – температура конденсации, К.

Коэффициент плотностиλ_пл учитывает уменьшение производительности из-за утечек и перетечек через всасывающие, нагнетательные клапаны, поршневые кольца, которые также, как и потери от подогрева, являются «скрытыми» потерями и не отображаются на индикаторной диаграмме. Коэффициент плотности зависит от отношения давлений и для современных поршневых компрессоров находится в пределах λ_пл = (0,95 – 0,99).

Важнейшей характеристикой, учитывающей все объемные потери реального компрессора является коэффициент подачи λ, который показывает во сколько раз его действительная массовая производительность G_а меньше теоретической G_ат

λ = 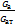(2. 12)

Коэффициент подачи также можно представить в виде произведения всех выше рассмотренных объемных коэффициентов

λ = λ_cλ_дрλ_ωλ_пл (2. 13)

Если отнести состояние всасываемого пара к теоретической точке 1 (рис.2.17,а ), то выражение (2.12) преобразуется в отношение действительной V_ди теоретической V_ц объемных производительностей компрессора

λ = 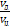, (2. 14)

Холодопроизводительность компрессора можно получить, решая совместно выражения (2.14) и (2.5) с учетом того, что V_д = G_аv₁, где v₁ – удельный объем всасываемого пара в (.) 1 на индикаторной диаграмме (рис. 2. 17,б)

= V_цq_v /λ (2 15)

где q_v = q₀/v₁ – удельная объемная холодопроизводительность хладагента.

Выражение (2.15) показывает, что для одного и того же компрессора (V_ц = const) могут быть различные значения холодопроизводительности Q₀, в зависимости от значений q_v и λ, которые в свою очередь зависят от температуры кипения и конденсации. Поэтому заводские значения холодопроизводительности даются для вполне определенных, стандартных условиях. При этих условиях температура кипения t₀ принимается равной - 15⁰C, температура конденсации t_k = +30⁰C, а переохлаждение хладагента перед дросселем ∆t равно 5⁰C. Тогда, учитывая выражение (2.15) пересчет стандартной холодопроизводительности на рабочие условия проводится следующим образом:

для стандартных условий

Q_{0 ст} = V_цq_vстλ_ст (2.16)

для рабочих условий

Q_{0 р} = V_цq_vрλ (2.17)

Отсюда

Q_{0 р} = Q_{0 ст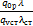} (2.18)