Приближенные вычисления и вычисления формул

Погрешности и аппроксимации. Во всех задачах, где необходимо рассчитать расстояние, время, массу или другие количественные величины, нельзя вычислить точный ответ, можно лишь определить его с заданной степенью точности. Чтобы учесть это обстоятельство, используют понятие так называемой погрешности измерения.

Для учета погрешности измерения ответ, как правило, ограничивают таким образом, чтобы в результате было максимум на одну значащую цифру больше, чем в исходных данных.

В десятичных дробях может возникнуть погрешность округления. Например, утверждать, что π = 3.142, не совсем верно; правильным будет следующее утверждение: π = 3.142 с точностью до 4 значащих цифр (в действительности π = 3.14159265...).

Некорректное выполнение действий может привести к неправильному результату вычисления. Такой результат называют ошибочным.

Если в результате вычисления неправильно расположена десятичная точка, говорят, что допущена ошибка в порядке величины.

Вероятность ошибок вычисления можно уменьшить путем аппроксимации, определив приблизительные результаты вычислений. Если ответ выглядит неправильным, его следует проверить, и при необходимости вычисление следует повторить.

Инженеру часто требуется производить в уме приблизительные расчеты. Например,

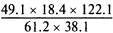можно упростить до 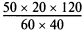, а затем сократить. В результате получим

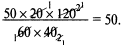
Следовательно, точный ответ лежит где-то в пределах 45...55. Разумеется, он не может равняться 5 или 500. Действительно, произведя вычисления с помощью калькулятора, получаем, что

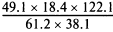= 47.31 с точностью до 4 значащих цифр.

Калькулятор. Сегодня карманный электронный калькулятор — наиболее современное подспорье для проведения вычислений. С его помощью можно быстро выполнять вычисления с точностью до 9 значащих цифр. Появление инженерного калькулятора сделало почти ненужными таблицы и логарифмы. Чтобы убедиться, хорошо ли вы управляетесь с калькулятором, проверьте ответы к следующим вычислениям:

Таблицы преобразований и диаграммы. Довольно часто вычисления приходится выполнять с помощью различных таблиц преобразований и диаграмм. Это относится, например, к курсам иностранных валют, переводу британских единиц измерения в метрические, производственным графикам и так далее.

Пример. В Табл. 1.1 показан перевод некоторых величин из британской системы единиц в метрическую.

42 кг = 42 х 2.2 фунта = 92.4 фунта, 0.4 фунта = 0.4 х 16 унций = 6.4 унции = 6 унций с точностью до унции.

Таким образом, 42 кг = 92 фунта 6 унций с точностью до унции.

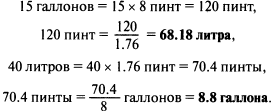
Вычисления формул. Говорят, что выражение вида υ = u + at есть формула для υ, выраженного через и, a и t, где υ, и, а и t — обозначения переменных.

Единственная величина в левой части выражения, υ, называется искомой величиной.

Если заданы численные значения всех переменных формулы, кроме одной, эта переменная становится искомой величиной и может быть вычислена с помощью калькулятора.

Пример. Пусть скорость и задана в виде υ = u + at. Определить υ с точностью до 3 значащих цифр при u = 9.86 м/с, а = 4.25 м/с², t = 6.84 с:

υ = и + at = 9.86 + (4.25) (6.84) = 9.86 + 29.07 = 38.93.

Следовательно, скорость υ = 38.9 м/с с точностью до 3 значащих цифр.

Пример. Объем прямого кругового конуса V см³ задается формулой V = 1/3πr²h. Определить объем с точностью до 4 значащих цифр, если r = 4.321 см, а h = 18.35 см:

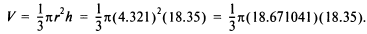
Следовательно, объем V = 358.8 см³ с точностью до 4 значащих цифр.

Следовательно, сила F = 1.49 х 10^-11 Н с точностью до 3 значащих цифр.