Использование алгебраических преобразований в параллельных вычислениях

Пример №2.6. Пусть требуется вычислить величину:
X₂₆ = a²c─5abc─a²d + b²c + 5abd─b²d (2.9)

ПФ непосредственного решения этой задачи на 4-процессорной ПВМ (p = 4) можно представить в виде табл.2.5:

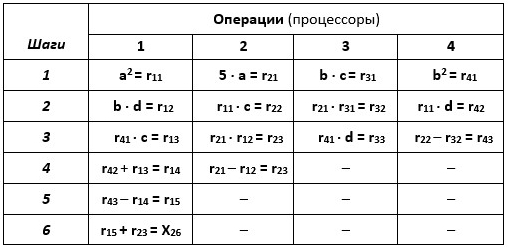
Табл. 2.5. Вычисление величины X26 на 4-процессорной ПВМ (Пример №2.6)

Как отмечалось выше, различные порядки выполнения операций и различные разбиения операций на группы порождают различные ПФ. Поэтому ПФ, представленная в табл.2.5, может быть и не оптимальной с точки зрения ее минимальной высоты.

Определим характеристики алгоритма, ПФ которого представлена в табл.2.5:
а) ускорение S₄ = H₁ / H₄ = 16 / 6 = 2,67;
б) эффективностьE₄ = 2,67 / 4 = 0,667;
в) высота H₄ = 6;
г) загруженность процессоров : Z₄ = (16 / 24) 100% = 66,7%.

Вопрос об устойчивости параллельных алгоритмов был рассмотрен выше.Таким образом, для вычисления величины X₂₆ (2.9) необходимо осуществить 6 шагов и выполнить 16 операций. Однако выражение для X₂₆ путем алгебраических преобразований можно представить в виде:
X^*₂₆ =(a²c + 5abc + b²c) – ( a²d + 5abd + b²d ) =
= ( a² + 5ab + b²) c – ( a² + 5ab + b²) d )=
= [( a² + 5ab + b²) ( c – d )] = [( a² + 2ab + b²) + 3ab] ( c – d ).

Окончательно в результате преобразований получим:
X*₂₆ = [( a + b )² + 3ab] ( c – d ) (2.10)

ПФ вычисления величины X*₂₆на 4-процессорной ПВМ можно представить в виде табл.2.6:

Табл. 2.6. Вычисление величины X*26 на 4-процессорной ПВМ (Пример №2.6)

Определим характеристики алгоритма, представленного в ПФ табл.2.6:
а) ускорение S₄ = H₁ / H₄ = 7 / 4 = 1,75;
б) эффективностьE₂ = 1,75 / 4 = 0,44;
в) высота H₂ = 4;
г) загруженность процессоров: Z₄ = (7 / 16) 100% = 43,7%.

Таким образом, для решения поставленной задачи (Пример №2.6) с использованием алгебраических преобразований понадобилось осуществить лишь 4 шага и выполнить 7 операций для вычисления величины X*₂₆(2.10).

Теперь построим ПФ алгоритма решения той же задачи на 2-процессорной ПВМ (табл.2.7).

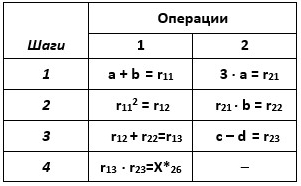
Табл. 2.7. Вычисление величины X*26 на 2-процессорной ПВМ (Пример №2.6)

Определим характеристики алгоритма, представленного в ПФ табл.2.7:
а) ускорение S₂ = H₁ / H₂ = 7 / 4 = 1,75;
б) эффективностьE₂ = 1,75 / 2 = 0,875;
в) высота H₂ = 4;
г) загруженность процессоров : Z₂ = (7 / 8) 100% = 87,5%.

Сравнивая алгоритмы вычислений в ПФ табл.2.6 и табл.2.7, можно видеть, что для решения поставленной задачи следует использовать 2-процессорную ПВМ, поскольку она имеет лучшие характеристики (эффективность и загруженность) по сравнению с 4 - процессорной ПВМ.

Пример №2.7. Пусть требуется вычислить величину:
X₂₇ = [a³ + 4 a b (a – b) – b³] [ c³ – 4 c d (c – d) + d³ ] (2.11)

Для непосредственного вычисления величины X₂₇(2.11) на 4-процессорной ПВМ необходимо осуществить 8 шагов и выполнить 21 операцию. Преобразуем выражение для X₂₇:
X₂₇ =(a³ + 4a² b – 4ab² – b³) ( c³ – 4c² d – 4cd² + d³ ) =
= (a³ + 5a² b – a² b – 5ab² + ab² – b³) ( c³ – 5c² d + c² d – 5cd² + cd² + d³ ) =
= [(a³ + 2a² b + ab²)– (a² b + 2ab² + b³) + (3a² b – 3ab² )] ×
× [( c³ – 2c² d + cd² ) + (c² d – 2cd² + d³) – ( 3c² d +3cd² )] =
= [ а (a + b)² – b ( a + b)² + 3ab (а – b)] [ c (c – d )² + d (c – d)² – 3cd (с + d )] .

В результате преобразований получим:
X₂₇ = { [ ( a + b )² + 3ab] ( a –b) } { [ ( c – d )² – 3cd ] (c + d) }(2.12)

ПФ вычисления величины X₂₇ на 4-процессорной ПВМ представлена в табл.2.8.

Табл. 2.8. Вычисление величины X27 на 4-процессорной ПВМ (Пример №2.7)

Определим характеристики алгоритма, представленного в ПФ табл.2.8:
а) ускорение S₄ = H₁ / H₄ = 15 / 5 = 3;
б) эффективностьE₂ = 3 / 4 = 0,75;
в) высота H₂ = 5;
г) загруженность процессоров: Z₄ = (15 / 20) 100% = 75%.

Таким образом, для решения поставленной задачи (Пример №2.7) с использованием алгебраических преобразований понадобилось осуществить лишь 5 шагов и выполнить 15 операций для вычисления величины X₂₇(2.12).