Основы реперного формализма в декартовой системе координат.

Здесь рассмотрим понятия локального репера, векторного элемента длины и теорему Пифагора в декартовых координатах.

Рассмотрим произвольную точку 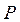, положение которой в пространстве определяется его радиус-вектором:

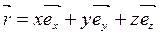. (1.1)

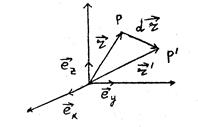
Рис.1

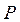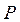Если ввести близкую к точку ’ с координатами 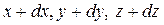, то разность радиус-векторов положения этих двух точек определяет бесконечно малый вектор, называемый векторным элементом длины.

Из (1.1) следует, что

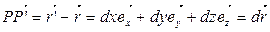. (1.2)

Это соотношение можно объяснить как разложение вектора 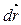по декартовому базису из единичных векторов .

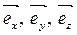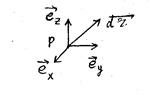
Рис.2

С другой стороны, (1.2) можно получить дифференцированием (1.1), считая 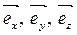постоянными величинами. Таким образом, в каждой точке пространства имеется тройка взаимно-перпендикулярных единичных векторов 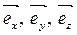с общим началом, причем они при переходе из одной точки в другую сохраняют свою длину и направление. Множество всех векторов ( 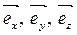) называется локальным декартовым репером.

Из (1.1) следует, что

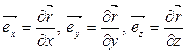. (1.3)

Квадрат расстояния между близкими точками определяется теоремой Пифагора

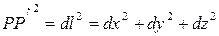. (1.4)

Это соотношение можно получить из (1.2), используя таблицу скалярных произведений декартова репера:

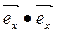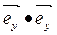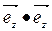= = = 1

(1.5)

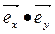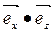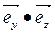= = = 0

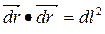. (1.6)

Следовательно, таблица скалярных произведений (1.5) эквивалентна теореме Пифагора (1.4), и позволяет определить важный геометрический объект, называемый метрическим тензором. Введем индексные обозначения:

;

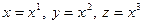(1.7)

.

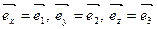Кроме того, определим символ Кронекера:

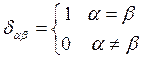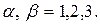, где (1.8)

Тогда таблица скалярных произведений декартова репера (1.5) записывается в форме:

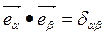(1.9)

Таким образом, метрическим тензором называется тензор второго ранга, компоненты которого в декартовой системе координат совпадают с символом Кронекера.