Арифметические операции над числами с фиксированной точкой

Сложение (вычитание).Операция вычитания приводится к опера­ции сложения путем преобразования чисел в обратный или дополни­тельный код. Пусть числа А≥0 и В≥0, тогда операция алгебраическо­го сложения выполняется в соответствии с табл. 2.3.

Таблица преобразования кодов при алгебраическом сложении Таблица 2.3

Скобки в представленных выражениях указывают на замену опера­ции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществ­ляется последовательно, поразрядно в соответствии с табл. 2.2. При вы­полнении сложения цифр необходимо соблюдать следующие правила.

1. Слагаемые должны иметь одинаковое число разрядов. Для вы­равнивания разрядной сетки слагаемых можно дописывать незнача­щие нули слева к целой части числа и незначащие нули справа к дроб­ной части числа.

2. Знаковые разряды чисел участвуют в сложении так же, как и значащие.

3. Необходимые преобразования кодов (п.2.3.1) производятся с из­менением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.

4. При образовании единицы переноса из старшего знакового раз­ряда, в случае использования ОК, эта единица складывается с млад­шим числовым разрядом. При использовании ДК единица переноса те­ряется. Знак результата формируется автоматически, результат пред­ставляется в том коде, в котором представлены исходные слагаемые.

Пример 2.9.Сложить два числа: A₁₀=7; B₁₀=16.

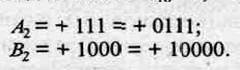
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:

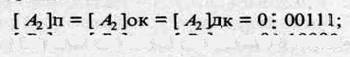
Сложение в обратном или дополнительном коде дает один и тот же результат:

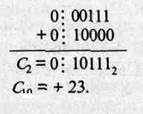
Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата.

Пример 2.10.Сложить два числа:A₁₀ = + 16; В₁₀ = -7 в ОК и ДК. В соответствии с табл. 2.3 должна быть реализована зависимость А+(-В), в которой второй член преобразуется с учетом знака

При сложении чисел в ОК и ДК были получены переносы в знако­вый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см. п.4 правил). В случае ДК этот перенос игнорируется.

Умножение.Умножение двоичных чисел наиболее просто реали­зуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.

Пример2.11. Умножить два числа А₁₀=7;В₁₀=5. Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.

Нетрудно видеть, что произведение получается путем сложения частных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на нуль, игнорируют­ся. Важной особенностью операции умножения и-разрядных сомножи­телей является увеличение разрядности произведения до п+п=2п. Знак произведения формируется путем сложения знаковых разрядов сомно­жителей. Возможные переносы из знакового разряда игнорируются.

Деление.Операция деления, как и в десятичной арифметике, явля­ется обратной операции умножения. Покажем, что и эта операция приводится к последовательности операций сложения и сдвига.

Пример 2.12.Разделить два числа A₁₀ ⁼ 45; В₁₀ = 5.

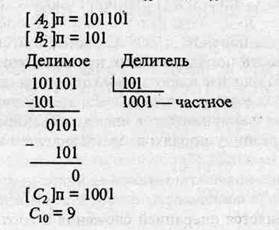
Деление произведено так же, как это делается обычно в десятич­ной системе. Сначала проверяется, можно ли вычесть значение дели­теля из старших разрядов делимого. Если возможно, то в разряде час­тного записывается единица и определяется частная разница. В противном случае в частное записывается нуль и разряды делителя сдви­гаются вправо на один разряд по отношению к разрядам делимого. К полученной предыдущей разнице сносится очередная цифра делимо­го, и данный процесс повторяется до тех пор, пока не будет получена необходимая точность. Если учесть, что все вычитания в ЭВМ заме­няются сложением в ОК или ДК (см. табл. 2.3), то действительно опе­рация деления приводится к операциям сложения и сдвигам вправо разрядов делителя относительно разрядов делимого. Отметим, что делимое перед операцией деления должно быть приведено к 2n-разрядной сетке. Только в этом случае при делении на n-разрядный дели­тель получается n-разрядное частное.

Знак частного формируется также путем сложения знаковых раз­рядов делимого и делителя, как это делалось при умножении.