Алгебраическая форма комплексного числа
Число 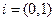 называется мнимой единицей.
называется мнимой единицей.
Квадрат мнимой единицы представляет собой вещественное число, равное -1:
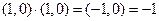 .
.
Тогда для любого числа 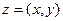 имеем
имеем
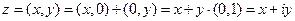 .
.
Это алгебраическая форма комплексного числа.
Пусть 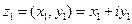 и
и 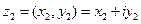 , тогда
, тогда
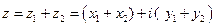 ,
,
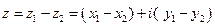 ,
,
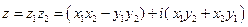 ,
,
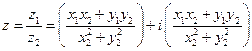 .
.
1.4. Сопряжение.Пусть 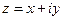 .
.
Сопряженное к z число: 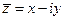 .
.
Свойства операции сопряжения:
1. 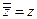 ;
;
2. 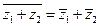 ;
;
3. 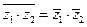 ;
;
4. 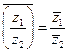 ;
;
5. 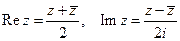 .
.
1.5. Тригонометрическая форма записи комплексных чисел.Точка 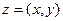 на плоскости может быть задана не только декартовыми, но и полярными координатами
на плоскости может быть задана не только декартовыми, но и полярными координатами 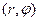 :
:
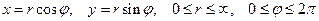 .
.
Число r называется модулем числа z, 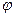 - аргументом:
- аргументом:
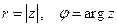 .
.
Рис.2.
Аргумент определен неоднозначно (с точностью до 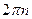 ), поэтому различают
), поэтому различают
(1) главное значение аргумента 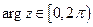 или
или 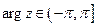 ;
;
(2) (многозначный) аргумент 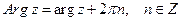 ; используются также записи
; используются также записи
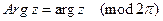 ,
, 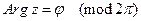 .
.
Комплексное число можно записать в виде
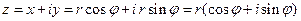
Это – тригонометрическая форма записи комплексных чисел.
Перемножим два числа:
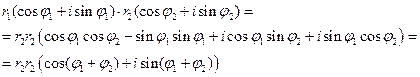
Таким образом,
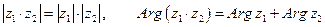 .
.
1.6. Формула Эйлера. Рассмотрим функцию
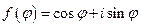 .
.
Она обладает свойством
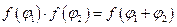 .
.
Эта функция обозначается 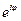 :
:
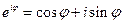 ;
;
Это – формула Эйлера.
Средствами анализа можно доказать, что функция действительно является показательной функцией.
Показательная форма записи комплексных чисел:
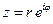 ,
,
где
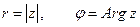 .
.
Из формулы Эйлера получаем:
 ;
;
Складывая/вычитая эти равенства находим
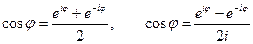 .
.
1.7. Возведение в степень. Тригонометрическая и показательная формы записи полезны при возведении комплексных чисел в степень:
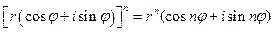 .
.
Дата добавления: 2016-07-27; просмотров: 1842;











