Определение деформации чистого сдвига

Чистым сдвигом называется такой вид деформирования бруса, при котором на гранях выделенного элементарного параллелепипеда действуют лишь касательные напряжения. Нормальные напряжения на этих гранях равняются нулю.

Явление чистого сдвига тяжело осуществить внешними действиями, потому что оно всегда сопровождается другими видами деформации, такими как изгиб, смятие и тому подобное.

Теоретически можно доказать, что при некоторых условиях нагружения бруса существуют такие взаимно перпендикулярные площадки, на которых отсутствующие нормальные напряжения, а действуют лишь касательные напряжения.

Рассмотрим частный, но очень важный для практики случай, когда на элемент бруса в виде параллелепипеда, в основе которого лежит квадрат, а боковые грани перпендикулярные плоскости чертежа, действуют в двух взаимно-перпендикулярных направлениях нормальные напряжения, равные по величине и противоположные по направлению. Допустим, что в горизонтальном направлении действуют напряжение растяжения σ_x , а в вертикальном направлении действуют напряжение сжатия σ_y. при этом σ_y = - σ_x (рис.10.1,а). Проведем через середины сторон основания параллелепипеда прямые, наклоненные к этим сторонам под углом 45⁰. Получим квадрат abcd, который является основанием нового элементарного параллелепипеда. На гранях этого параллелепипеда будут действовать лишь касательные напряжения τ (приводим без доказательства), которые численно равняются нормальным напряжением, что действуют на горизонтальных и вертикальных гранях первого параллелепипеда, то есть:

τ = σ_x = - σ_y(10.1)

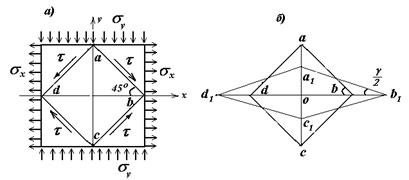
Рис.10.1

При этом касательные напряжения направлены от напряжений сжатия в сторону напряжений растяжения, как показано на рис.10.1,а.

Такое напряженное состояние параллелепипеда имеет название чистый сдвиг.

10.2. Деформация сдвига. Закон Гука при сдвиге.

Модуль сдвига действуют на горизонтальных и вертикальных гранях первого паралелепипела, показано на рис.фофо

Рассмотрим деформацию элемента abcd при сдвиге, то есть от действия касательных напряжений. Поскольку нормальные напряжения на гранях отсутствуют, то длины сторон ab, bc, cd и ad не будут изменяться, но вертикальная диагональ получит некоторое укорочение, а горизонтальная диагональ получит соответствующее удлинение. В результате квадрат превратится в ромб a₁b₁c₁d₁. Угол при вершине b, который до деформации был прямым, уменьшится на некоторую величину γ,то есть будет равняться π/2 - γ, а угол при вершине а увеличится на такую же величину и станет ровным π/2 + γ . Угловая величина γназывается относительным сдвигом, или углом сдвига.

Если материал тела является идеально упругим, то относительный сдвиг γ будет прямо пропорциональным касательному напряжению τ, то есть:

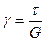(10.2)

где G – некоторый коэффициент пропорциональности, величина которого зависит от механических свойств материала. Величина G называется модулем упругости при сдвиге или модулем второго рода. Напомним, что модулем первого рода является модуль продольной упругости E. Размерностью модуля упругости является паскаль (Па), или кратные величины: килопаскаль (кПа), и мегапаскаль (МПа).

Модуль сдвига G для изотропных материалов зависит от модуля продольной упругости E и коэффициента Пуассона μ. Как известно этот коэффициент равняется отношению, взятому с отрицательным знаком, относительной поперечной деформации 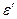к относительной продольной деформации 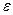, т.е.

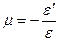
Для установления зависимости между указанными тремя константами, рассмотрим треугольник oab (рис.10.1,б), угол при вершине b которого равняется π/4. От действия касательных напряжений сторона ob получит некоторое удлинение и станет равной ob₁, а сторона oa получит соответствующее укорочение и станет равной oa₁. При этом:

ob₁= ob(1+ε_x), а oa₁ = oa(1+ε_y)

Заметим, что деформации сторон треугольника являются очень малыми по сравнению с размерами этих сторон и только с целью показать наглядно чертеж, эти деформации значительно увеличены.

Найдем тангенс угла при вершине b треугольника oab. Этот угол равняется π/4 – γ/2. Тогда:

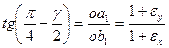(10.3)

Раскроем тангенс разности двух углов и учтем, что для очень малых углов γ существует равенство этих углов и их тангенсов. В результате получим:

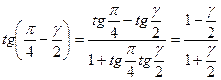(10.4)

Пользуясь принципом независимости действия нормальных напряженийσ_x иσ_yи учитывая, чтоτ = σ_x = - σ_y, найдем относительные деформации ε_x и ε_y.

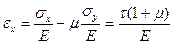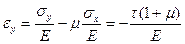и (10.5)

Приравняем правые части выражений (10.3) и (10.4 ) и заменим относительные линейные деформации их значениями согласно зависимостей (10.5), в результате получим:

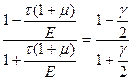
Это равенство возможно при условии, что .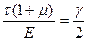

Учитывая, что 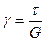, найдем:

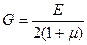(10.6)

Таким образом, полученная формула устанавливает связь между тремя упругими характеристиками материала: модулями упругости при сдвиге и при растяжении, а также коэффициентом Пуассона. Из этой формулы видно, что модуль упругости при сдвиге имеет меньшее значение, чем модуль упругости при растяжении (сжатии). Например, для стали при μ=1/3 имеем: G=3/8E. Это означает, что сопротивление материалов сдвигу слабее, чем их сопротивление растяжению (сжатию).

10.3. Расчетное сопротивление при сдвиге.

Условие прочности

Раньше было сказано, что чистого сдвига в природе не существует, но его можно смоделировать и установить зависимость между касательным напряжением τ и относительным углом сдвига γ. Эта зависимость может быть начерчена в виде диаграммы, которая напоминает диаграмму растяжения. То есть она имеет предел пропорциональности, предел текучести и предел прочности. Но эти значения несколько меньше соответствующих значений, полученных в результате испытания образцов на растяжение, в частности, для стали

τ_т=(0.55 – 0.60)σ_т.

Как и для задачи растяжения, при сдвиге вводится понятие расчетного сопротивления, которое определяется по отношению к пределу текучести τ_т с использованием коэффициентов однородности, условий работы и перегрузки. Расчетное сопротивление материала сдвигу обозначается символом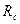

Если принять те же значения трех коэффициентов, что приняты для случая растяжения стержня, то получим:

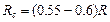
Таким образом, расчетное сопротивление сдвигу значительно меньше расчетного сопротивления при растяжении. Это обстоятельство нужно учитывать при решении практических задач на сдвиг.

Рабочие касательные напряжения, которые возникают при сдвиге, не должны превышать расчетного сопротивления. В результате условие прочности при сдвиге принимает вид:

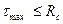(10.7)

В инженерной практике встречаются многие важные задачи, для решения которых может быть использована теория чистого сдвига. К таким задачам относятся:

- расчет болтовых соединений;

- расчет заклепочных соединений;

- расчет сварных соединений.

В следующих параграфах будем рассматривать последовательно решение этих задач.

10.4. Расчет болтовых соединений

Рассмотрим случай, когда нужно объединить два металлических стержня в один так, чтобы их ось располагалась на одной прямой. Для этого можем использовать болтовое соединение, которое показано на рис.10.2. Обозначим диаметр болта через d.

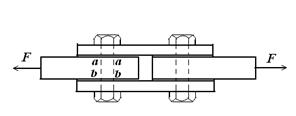
Рис.10.2

При загружении соединения силами растяжения F возникает деформация сдвига в двух плоскостях (в поперечных сечениях болта а-а и b-b). При этом силы сдвига в каждом сечении равняются половине внешней силы, то есть F/2. Болт имеет круглую форму поперечного сечения и поэтому площадь сечения определяется по известной формуле:

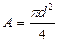(10.8)

При расчете болтовых соединений принимается допущение о равномерности распределения касательных напряжений в площади поперечного сечения болта. Тогда рабочие касательные напряжения в одном сечении болта будут равняться:

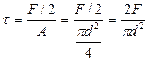(10.9)

Используем условие прочности болта (10.7), т.е условие 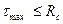, получим:

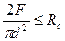, откуда 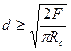(10.10)

10.5. Расчет заклепочных соединений

Более технологичными соединениями металлических конструкций, в сравнении с болтовыми соединениями, являются заклепочные соединения. Они широко используются, в частности, в деталях конструкций самолета, которые несут динамические нагрузки, а также в мостовых фермах и других сооружениях.

При расчете заклепочных соединений принимаются допущения:

1) толщины соединяемых листов достаточно малы по сравнению с их линейными размерами, что позволяет пренебречь возможными при этом эффектами изгиба;

2) продольные усилия, которые возникают в листах, равномерно передаются на все заклепки соединения и касательные напряжения также равномерно распределяются в поперечных сечениях заклепок.

Заклепочные соединения изготовляются в заводских условиях. Заклепки нагревают до высоких температур, устанавливают в отверстия листов, которые объединяются и формируют головки с помощью пресса. При охлаждении заклепок возникает сжатие соединяемых листов и между ними появляются силы трения. Поэтому заклепки начинают работать на сдвиг подобно болтам лишь после того, как будут преодолены силы трения между листами. Расчет заклепочных соединений при этом значительно осложняется и для его упрощения приходиться пренебрегать силами трения.

Таким образом, инженерный расчет заклепочных соединений не отличается от расчета болтовых соединений и выполняется в зависимости от количества заклепок и количества плоскостей сдвига (плоскостей среза заклепок).

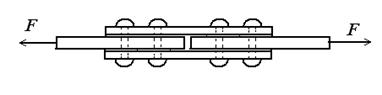
Рис.10.3

На рис.10.3 представлено соединение двух стержней с помощью двух накладок и четырех заклепок, расположенных в один ряд. Каждый стержень крепится двумя заклепками (количество заклепок обозначается буквой m), а каждая заклепка имеет два среза подобно болту, рассмотренному в предыдущем параграфе (количество срезов одной заклепки обозначается буквой n).

Таким образом, общая площадь среза (сдвига) произвольного количества заклепок будет равняться:

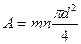(10.11)

Учитывая, что 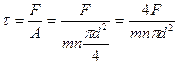, и используя условие прочности 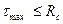, найдем необходимую величину диаметра заклепки:

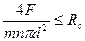, откуда 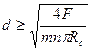(10.12)

Выполняя расчет заклепочного соединения, нужно иметь в виду, что заклепки ослаблюють поперечное сечение листов (стержней), которые соединяются. Поэтому, при определении нормальных напряжений в поперечном сечении и проверке прочности листов стержня, нужно принимать площадь ослабленного сечение .

Кроме того, заклепки испытывают смятие по поверхностям их соприкасания со стенками отверстий стержня. Если наименьшая толщина листа равняется h, то площадь смятия одной заклепки будет равняться:

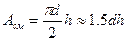(10.13)

Сила растяжения F равномерно распределяется между всеми заклепками, поэтому, если соединение содержит m заклепок, то на каждую из них будет действовать сила смятия равная F/m.

Нормальные напряжения смятия определяются отношением силы смятия к площади смятия, то есть:

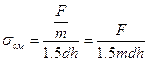(10.14)

Эти напряжения не должны превышать расчетного сопротивления при смятии. В результате получаем условие прочности заклепки при смятии:

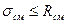(10.15)

Расчетное сопротивление при смятии имеет больше значения, чем при растяжении, и определяется зависимостью: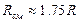

Если нормальные напряжения смятия, определенные по формуле (10.14) превышают расчетное сопротивление, то нужно увеличить толщину объединяемых листов, или диаметр заклепки.

При изготовлении заклепочных соединений принимают шаг заклепок в любом направлении равным 3-4 диаметрам этих заклепок. Расстояние от края листа до первого ряда заклепок принимаются равным 2-3 диаметрам заклепок.

10.6. Расчет сварных соединений

Сварные соединения имеют значительные преимущества перед заклепочными и болтовыми соединениями. Эти преимущества касаются экономии металла из-за отсутствия ослаблений поперечных сечений отверстиями, выбора средств производства, большей компактности и простоты стыков, а также уменьшения трудоемкости работ при изготовлении сварных конструкций.

Сварные соединения за прочностью не уступают заклепочным соединениям при действии на них как статических, так и динамических нагрузок. Особенно быстрых темпов приобрело внедрения в производство сварных соединений в середине ХХ века благодаря научным трудам советских ученых в отрасли автоматической сварки, и сварки под флюсом.

Сварные соединения выполняются в стык или внахлёстку. Если металлические листы, трубы, или стержни другой формы поперечных сечений, объединяются с помощью сварки в одной плоскости (рис.10.4), то имеет место стыковое соединение, а образованный сварной шов называется стыковым швом.

В зависимости от толщины свариваемых листов (труб, стержней), стыковые швы могут иметь три разных типа: прямой, V- подобный и X- подобный. Первый тип стыкового шва применяется при толщине свариваемых элементов до 8 мм. Второй – при их толщине от 8 до 25 мм, а третий – если толщина элементов превышает 25 мм На рис.10.4 показаны эти типы сварных швов.

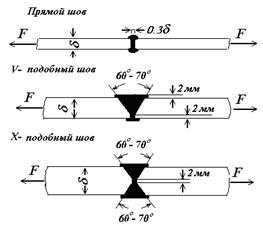
Рис.10.4

Если сварка элементов конструкции стыковыми швами осуществляется электродами с качественными (толстыми) обмазками, то расчет стыкового шва не выполняется. Прочность такого шва принимается равной прочности основного элемента. В других случаях расчет стыкового шва выполняют на основе условия прочности шва на растяжение или сжатие. Площадь стыкового шва принимается равной произведению расчетной длины шва 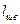на его высоту δ. При этом высота шва принимается равной толщине свариваемых элементов, а расчетная длина шва принимается на 2 см короче ширины листов.

То есть: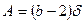

Нормальное напряжение, которое возникает в поперечном сечении стыкового шва, определяется по известной формуле и не должно превышать расчетного сопротивления :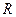

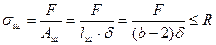(10.16)

расчетное сопротивление 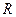на растяжение или сжатие шва принимаются по нормативным таблицам в зависимости от типа применяемых электродов.

При сварке элементов конструкции внахлёстку, используют валиковые сварные швы. Они могут быть торцевыми (лобовыми) или боковыми (фланговыми).

На рис.10.5 представлено сварное соединение внахлёстку двух листов с использованием лобовых валиковых швов. Эти швы имеют округлую форму, но при расчете они принимаются спрямленными. В случае растяжения или сжатия соединения, в биссекторной плоскости шва возникают наибольшие касательные напряжения сдвига (среза), то есть валиковый шов разрушается от действия касательных напряжений, а не от действия нормальных напряжений, возникающих в результате растяжения или сжатия элементов соединения.

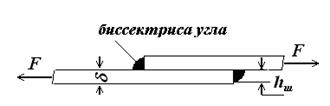
Рис.10.5

Расчетная высота валикового шва принимается равной 0,7h_шв, то есть 0,7 действительной высоты шва. Тогда площадь среза всех валиковых швов будет равняться 0,7h_шв 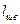. Где 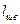есть общая длина швов. При известной высоте шва h_шв (она равняется приблизительно толщине листов, которые объединяются) условие прочности соединения будет иметь вид:

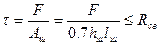(10.17)

Расчетная длина всех швов, определяется из приведенного условия, и будет равна:

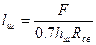(10.18)

Формула (10.18) используется также и при определении расчетной длины всех фланговых швов, или всех лобовых и фланговых швов соединения.

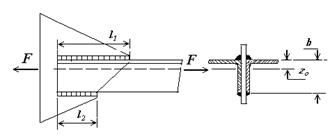
Рис.10.5

Рассмотрим случай, когда стержень из двух прокатних уголков присоединяется к фасонному листу с помощью фланговых швов (рис.10.5). Общая расчетная длина сварных швов определяется по формуле (10.18). Каждый уголок крепится к листу с помощью двух швов. Шва большей длины 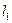и шва меньшей длины .

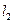Усилия, которые приходятся на каждый из двух швов, распределяются обратно пропорционально расстояниям их от линии действия силы F, которая проходит через центр тяжести поперечного сечения уголка. Следовательно, длина шва 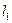, который находится ближе от центра тяжести, будет определяться отношением:

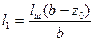(10.19)

Расчетная длина второго шва будет определяться по формуле:

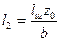(10.20)

Удвоенная сумма этих длин равняется расчетной длине всего шва, то есть

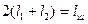(10.21)

Пример 10.1. Подобрать поперечное сечение стержня из двух равнополочных уголков и рассчитать его крепление к стального листу с использованием фланговых сварных швов, если сила растяжения стержня равняется 0,25 МН, а уголки изготовлены из стали марки Ст.3. Электроды имеют тонкую обмазку. Расчетное сопротивление на растяжение принять равным 200 МПа, а расчетное сопротивление сварного шва на срез – равным 110 МПа.

Решение задачи. Определяем необходимую площадь поперечного сечения стержня из условия прочности стержня на растяжение:

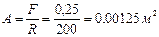, или A= 12,5 см²

Из таблиц сортамента прокатной стали находим два равнополочных уголка №7х0,45, общая площадь которых равняется:

A= 2·6,2= 12,4 см².

Поскольку толщина полки уголка равняется 0,45 см, то высоту шва принимаем равной 0,45 см. Общую длину шва определяем по формуле (10.18).

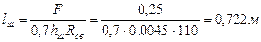
Для крепления одного уголка, нужно выполнить шов длиной 36,1 см (половина общей длины шва).

Расчетная длина шва, который расположен ближе от центра тяжести уголка будет равняться:

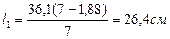, а длина шва, который расположен на большем расстоянии от центра тяжести уголка будет равняться: 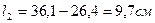(смотри рис.10.5).