При растяжении (сжатии) стержня

Рассмотрим прямой стержень, верхний торец которого закреплен с помощью жесткой опоры. Нагрузим его в нижнем торце осевой силой растяжения F, которая медленно изменяет свою величину от нуля до конечного значения F(рис.9.18,а). Такая нагрузка является статической. При медленном росте силы, также медленно растет абсолютная деформация стержня, то есть его удлинение 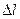и нормальные напряжения σ. Если нормальные напряжения не превышают предела пропорциональности, то сохраняется линейная зависимость между силой Fи удлинением стержня 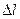(рис.9.18,б).

Статически нарастающая сила Fвыполняет определенную работу на соответствующем перемещении нижнего торца стержня. Чтобы определить эту работу, рассмотрим два безгранично близкие моменты времени роста силы и удлинения. Допустим, что для первого момента времени сила имеет значение F_x,а соответствующее удлинение имеет значение 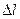_x ( левая граница заштрихованной части диаграммы 9.18,б). Для второго момента времени сила получит приращение dF_x, а удлинение стержня будет иметь приращение d 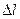_x (правая граница заштрихованной части диаграммы 9.18,б).

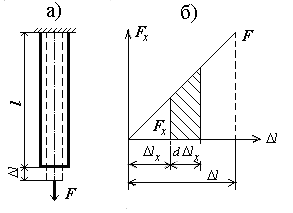
Рис. 3.18

Определим элементарную работу силы F_x + dF_x на перемещении d 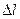_x, используя известную из физики формулу работы.

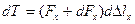(9.28)

Отбрасывая величины второго порядка малости, получим следующую формулу элементарной работы:

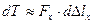(9.29)

Эта работа практически равняется площади заштрихованной части диаграммы (рис.9.18,б).

Полная работа, которую выполнит статически растущая сила F, будет равняться интегралу от элементарной работы (9.29) при изменении перемещения 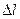_x в пределах от нуля до .

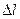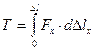(9.30)

Если напряжения не превышают предела пропорциональности, то согласно закону Гука имеем линейную зависимость между осевой силой и удлинением стержня, то есть:

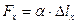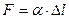и (9.31)

В зависимостях (9.31) a является коэффициентом пропорциональности. После подстановки (9.31) в (9.30) и интегрирования получаем:

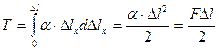, окончательно

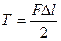(9.32)

Таким образом, работа статически нарастающей силы на соответствующем удлинении стержня равняется половине произведения конечного значения силы на конечное значение абсолютного удлинения стержня.

Это определение является теоремой Клапейрона.

Для определения работы внутренней продольной силы N можно использовать закон сохранения энергии. Если пренебречь составными частями энергии, такими, как тепловая и электромагнитная, то работа внутреннего усилия N (потенциальная энергия деформации стержня при растяжении или сжатии) будет равняться работе внешней силы, то есть:

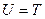(9.33)

Используя формулу (9,32) с учетом того, что F=N и удлинение стержня равняется:

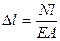(9.34)

найдем: 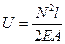(9.35)

Формула (3.34) дает возможность определить потенциальную энергию деформации стержня, если он имеет один участок, в пределах которого продольная сила и площадь поперечного сечения имеют постоянные значения. Если стержень содержит несколько участков, на которых внутренние усилия или площадь поперечного сечения стержня имеют разные величины, то потенциальная энергия определяется как сумма энергий, накопленных на каждом участке, то есть с использованием следующей формулы:

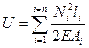(9.36)

Анализ полученных результатов позволяет сформулировать следующие свойства потенциальной энергии:

1) Потенциальная энергия всегда положительна, поскольку формула для ее определения содержит квадраты внутренних усилий.

2) Потенциальная энергия не зависит от последовательности приложения нагрузок, а зависит лишь от конечного состояния загружения стержня.

3) Потенциальная энергия суммы внешних сил не равняется сумме потенциальных энергий, вызванных каждой силой отдельно, то есть при определении потенциальной энергии нельзя использовать принцип независимости действия сил.

9.11 Задание для самостоятельной работы:

1) Тело весом F подвешено к потолку с помощью трех стальных стержней (рис.9.19). Определить усилия в стержнях и диаметры этих стержней, если

F= 250 кН, а площади поперечных разрезов всех стержней одинаковы.

2) Железобетонная колонна состоит из двух частей, имеющих разные площади поперечных сечений (рис.9.20).Она жестко закреплена сверху и снизу и нагружена силами 2F. Определить продольные усилия на каждой части колонны, если площадь поперечного сечения нижней части втрое больше от площади поперечного сечения верхней части. Определить напряжение при F=1,5 МН.

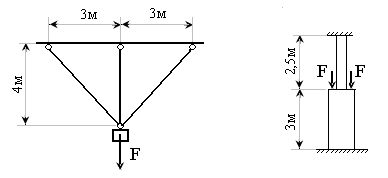
Рис.3.19 Рис.3.20

Вопросы для самоконтроля полученных знаний

1. В каком случае возникает центральное растяжение или сжатие стержня?

2. Какой метод используют для определения продольных сил в произвольном поперечном сечении стержня? В чем заключается этот метод?

3. Что такое эпюра продольных сил и как ее построить?

4. Как определяются продольные силы от действия собственного веса или равномерно распределенной нагрузки? Какой вид при этом имеет эпюра продольных сил?

5. Как определяются нормальные напряжения в поперечном сечении стержня при растяжении и сжатии? В чем заключается различие между этими напряжениями?

6. Что такое эпюра нормальных напряжений и как ее построить?

7. Как отличаются эпюры продольных сил и нормальных напряжений, если ступенчатый стержень нагружен сосредоточенными осевыми силами?

8. Как отличаются эпюры продольных сил и нормальных напряжений, если ступенчатый стержень нагружен равномерно распределенными осевыми силами?

9. Как определяются нормальные и касательные напряжения в наклоненных сечениях стержня? Докажите соответствующие формулы.

10. В каких сечениях стержня возникают наибольшие касательные напряжения?

11. В каких сечениях стержня возникают наибольшие нормальные напряжения?

12. Что такое абсолютная и относительная продольная деформация стержня? Единицы их измерения?

13. Что такое абсолютная и относительная поперечная деформация стержня? Единицы их измерения?

14. Какая зависимость существует между относительной продольной и относительной поперечной деформациями стержня? Как называется эта зависимость?

15. Что такое модуль продольной упругости Е? Единица его измерения? Как зависят деформации стержня от величины модуля упругости?

16. Что такое жесткость поперечного сечения стержня при его растяжении или сжатии?

17. Как формулируется закон Гука при растяжении или сжатии стержня?

18. Какой вид имеет обобщенная формула определения продольных деформаций стержня? Докажите эту формулу.

19. Какие характеристики материалов относятся к механическим характеристикам, а какие к пластичным?

20. Что такое упругие и остаточные деформации? В каком случае возникают только упругие деформации?

21. Что такое условный предел текучести? Для каких материалов он определяется?

22. Чем отличаются диаграммы растяжения стали и чугуна?

23. В каком случае перемещение поперечного разреза стержня совпадает с абсолютной деформацией?

24. Что такое допускаемое напряжение? Как оно определяется для пластичных и хрупких материалов?

25. Что такое коэффициент запаса прочности и как он определяется для пластичных и хрупких материалов?

26. Что такое расчетное сопротивление материалов? Как оно определяется?

27. Запишите условие прочности растянутого и сжатого стержня при расчете по методу расчетных сопротивлений.

28. Какие виды расчетов можно выполнить, используя условие прочности? Как выполняются эти расчеты?

29. Запишите условие жесткости стержня при растяжении и при сжатии.

30. Какие виды расчетов можно выполнить, используя условие жесткости? Как выполняются эти расчеты?

31. Какие системы относятся к статически неопределимым системам? что такое степень статической неопределимости системы?

32. В чем заключается расчет статически неопределимых систем?

33. Возникают ли напряжения в сечениях статически неопределимых систем от изменения температуры и неточностей изготовления стержней системы?

34. Что такое работа внешней силы, которая вызывает растяжение или сжатие стержня? Как она определяется?

35. Что такое потенциальная энергия деформации в случае растяжения или сжатия стержня? Как она определяется?

36. Приведите основные свойства потенциальной энергии.

37. Почему при определении потенциальной энергии нельзя использовать принцип независимости действия нагрузок?