При плоско поперечном изгибе

В предыдущем параграфе мы выяснили, что плоский поперечный изгиб балки возникает, если нагрузка действует в главной плоскости инерции сечения и направлена перпендикулярно оси балки. Реакции опор V_С, H_С и V_D определяются из условий равновесия балки, то есть из условий: 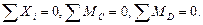При этом из первого условия равновесия находим величину H_С =0, а из второго и третьего определяем соответственно V_D и V_С

Рассмотрим некоторую балку, несущую поперечные нагрузки и допустим, что реакции опор этой балки уже определены (рис.11.3).

Для определения внутренних усилий, возникающих в произвольном поперечном сечении балки, используется метод сечений.

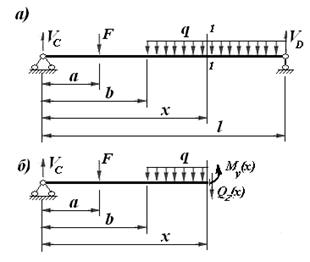
Рис. 11.3

Проведем произвольное поперечное сечение балки, взятое на переменном расстоянии xот начала координат. Начало координат всегда принимается на левом или на правом торце балки. В рассматриваемом примере начало координат совмещено с центром опоры А.

В этом сечении при поперечном изгибе возникает две составляющие внутренних усилий: поперечная сила Q_z(x), которая дает в плоскости разреза в направлении вертикальной оси z, и изгибающий момент M_y(x) относительно оси y, перпендикулярной плоскости действия нагрузки, то есть перпендикулярной осям xи z (рис.11.3,б).

Отбросим, мысленно, правую часть балки, и ее действие на левую часть, заменим внутренними усилиями Q_z(x) и M_y(x) , как показано на рисунке 11.3,б. Эта часть балки должна быть в равновесии, то есть для нее должны выполняться два условия равновесия:

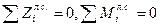
Составим два уравнения равновесия:

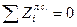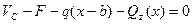: , откуда

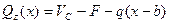(11.1)

Анализируя правую часть выражения (11.1) легко заметить, что поперечная сила, возникающая в произвольном сечении балки, равняется алгебраической сумме проекций всех нагрузок, которые действуют слева от сечения на вертикальную ось z.

Легко доказать, что поперечная сила в произвольном сечении балки равна алгебраической сумме проекций всех сил, расположенных справа от сечения на вертикальную осьzи взятых с противоположными знаками.

Поперечная сила принимается положительной, если она пытается повернуть какую-либо отрезанную часть балки в направлении движения часовой стрелки и отрицательной, если она действует наоборот (рис.11.4,а и б).

Внешняя нагрузка, которая действует относительно центра сечения балки по часовой стрелке, вызывает в этом сечении поперечную силу положительного знака (рис.11.5,а).

Внешняя нагрузка, которая действует относительно центра сечения балки против движения часовой стрелки, вызывает в этом сечении поперечную силу отрицательного знака (рис.11.5,б).

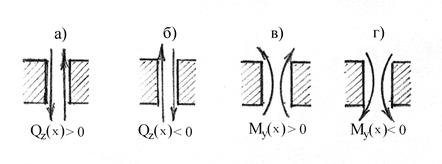
Рис. 11.4

Составим второе уравнение равновесия левой части балки (рис. 11.3,б). Для этого используем второе условие равновесия: :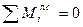

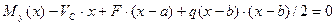, откуда

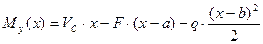(11.2)

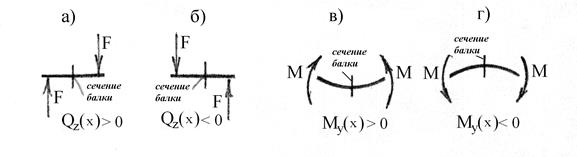
Рис. 11.5

Таким образом, изгибающий момент, который возникает в произвольном сечении балки, равняется алгебраической сумме моментов всех нагрузок, действующих слева от сечения, относительно оси y, которая проведена через центр сечения перпендикулярно плоскости нагрузки (или в расчетной схеме относительно центра поперечного сечения).

Изгибающий момент принимается с 1ние е ами.а вертикальную осьме положительным знаком, если он вызывает растяжение (удлинение) нижних волокон балки и с отрицательным знаком, если он вызывает растяжение верхних волокон балки (рис.11.4,в и г).

Нагрузка, которая действует слева от сечения и направлена по часовой стрелке относительно центра этого сечения, и нагрузка, которая действует справа от сечения и направлена против часовой стрелки относительно его центра, создает изгибающий момент положительного знака (рис.11.5,в).

Нагрузка, которая действует слева от сечения и направлена против часовой стрелки относительно его центра и нагрузка, которая действует справа от сечения и направлена по часовой стрелке относительно его центра, создает изгибающий момент отрицательного знака (рис.11.5,г).