Условия прочности и жесткости. Виды расчетов

Расчет растянутого или сжатого стержня на прочность и жесткость может осуществляться по участкам (в этом случае стержень будет иметь ступенчатую форму сечений) или для всего стержня (стержень постоянной жесткости).

В первом случае вычисляют рабочие напряжения, которые возникают в поперечных сечениях каждого участка стержня по известной формуле (9.2):

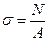(9.2)

Во втором случае по той же формуле вычисляют:

- наибольшие по модулю напряжения, если стержень изготовлен из упруго-пластических материалов (различных марок стали)

;

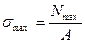- наибольшие растягивающие и наибольшие по модулю сжимающие напряжения, если стержень изготовлен из хрупких материалов (из чугуна, бетона, железобетона).

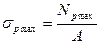
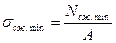
Эти напряжения не должны превышать определенной величины, установленной номами или техническими условиями для каждого вида материала и каждого вида деформирования элемента конструкции. В зависимости от метода расчета эту величину называют допускаемым напряжением или расчетным сопротивлением.

Если расчет осуществляется по методу допускаемых напряжений, то рабочее напряжение не может превышать допускаемого напряжения, которое обозначается символом .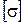

Допускаемые напряжения определяются отношением опасного напряжения к коэффициенту запаса прочности. За опасное напряжение принимается предел текучести 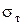для пластичных материалов, или предел прочности 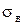для хрупких материалов.

Величины опасных напряжений определяют в результате испытания стандартных образцов пластичных материалов на растяжение, или в результате испытания стандартных образцов хрупких материалов на сжатие.

Коэффициент запаса прочности при растяжении бруса обозначается буквой 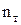, а при его сжатии буквой 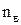. Эти коэффициенты имеют значения больше единицы и, в зависимости от условий эксплуатации конструкции, принимаются равными, в пределах: ; .

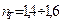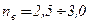Тогда, согласно приведенным выше определениям, допускаемое напряжение можно найти по формулам:

; .

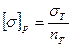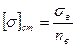Допускаемые напряжения регламентируются специальными нормами. Например, для различных марок стали, они имеют значения: 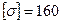- 180 МПа.

В результате получаем следующее условие прочности стержня по методу допускаемых напряжений:

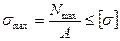(9.16)

Примечание: Условие (3.16) используется для материалов, которые имеют одинаковую прочность при растяжении и сжатии, то есть имеет равные значения допускаемых напряжений при растяжении и при сжатии. Если допускаемые значения напряжений при растяжении и сжатия имеют разные значения, то нужно рассматривать два условия прочности на растяжение и сжатие отдельно:

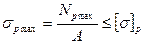(9.17)

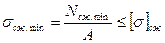(9.18)

Изложенный метод расчета в настоящее время практически не применяется, но он имеет историческую ценность и содержится в абсолютном большинстве учебников и учебных пособий по сопротивлению материалов.

Если расчет осуществляется по методу расчетных сопротивлений, то рабочее напряжение не может превышать расчетного сопротивления 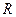, которое, как и допускаемое напряжение 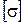, определяется с использованием предела текучести или временного сопротивления, принимаемых за нормативное сопротивление .

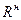Расчетное сопротивление определяется с использованием трех коэффициентов (коэффициента условий работы, коэффициента однородности материала и коэффициента перегрузки). Это приводит к более экономному расходу материала конструкции, так как значение расчетного сопротивления имеет больше значение чем допускаемое напряжение.

Например, для низкоуглеродистых сталей расчетное сопротивление принимается равным в пределах 210-240 МПа, тогда как допускаемое напряжение равно 160-180 МПа.

Условия прочности при растяжении (сжатии) приводятся к следующему виду:

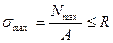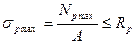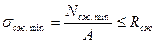, , (9.19)

В дальнейшем расчеты на прочность при любых видах деформирования стержней будем осуществлять по методу расчетных сопротивлений.

Условие прочности связывает между собой три величины:

- продольную силу N;

- площадь поперечного сечения А;

- расчетное сопротивление ,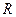

В соответствии с этим возможные три вида расчета стержня на прочность:

1. Проверочный расчет. Если известны все три величины: N, А, 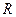, но отсутствуют расчеты стержня, то осуществляется проверка выполнения условия прочности. При выполнении этого условия стержень можно использовать по назначению, а при невыполнении условия прочности нужно увеличить площадь сечения стержня, или уменьшить нагрузку.

2. Определение размеров поперечного сечения: Эта задача сопротивления материалов является основной и имеет название проектного расчета. В этом случае известны продольная сила N и расчетное сопротивление 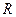. Необходимая площадь поперечного сечения определяется из условия прочности:

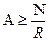. (9.20)

В зависимости от заданной формы сечения находятся его размеры.

3. Определение допускаемой нагрузки. В этом случае известны площадь поперечного сечения А и расчетное сопротивление 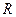. Тогда из условия прочности находим допускаемую продольную силу (допускаемую нагрузку на стержень):

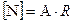. (9.21)

Условие жесткости стержня. В случае растяжения или сжатия стержень получает абсолютное удлинение или укорочение 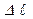. Величина этой деформации не может быть больше допускаемой деформации 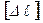, то есть

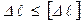,или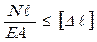(9.22)

Это условие называется условием жесткости стержня при растяжении или сжатии. Оно позволяет выполнить три вида расчетов стержня на жесткость, аналогично, как и при использовании условия прочности, то есть:

1. Осуществить проверку выполнения условия жесткости;

2. Определить размеры поперечного сечения;

3. Определить допускаемую нагрузку на стержень.