Вопрос для самоконтроля полученных знаний.

1. Какой вид напряженного состояния называется чистым сдвигом?

2. Какая зависимость существует между нормальными напряжениями на двух взаимно перпендикулярных плоскостях при чистом сдвиге?

3. Что такое плоскости чистого сдвига? Какие напряжения действуют на этих плоскостях?

4. Что называется относительным сдвигом?

5. Запишите формулу закона Гука при сдвиге.

6. Какая зависимость существует между модулем продольной упругости, модулем упругости при сдвиге и коэффициентом Пуассона?

7. Что такое модуль упругости материала при сдвиге? В каких единицах он измеряется?

8. Что такое коэффициент Пуассона?

9. Какие виды соединений элементов конструкций Вы знаете?

10. Как выполняется болтовое соединение?

11. В чем заключается расчет болтового соединения?

12. Какие напряжения возникают в разрезе болта? Как они определяются?

13. Что такое допускаемое напряжение на сдвиг (срез)?

14. Запишите условие прочности болта на срез.

15. Как выполняется заклепочное соединение? Чем оно отличается от болтового соединения?

16. Как выполняется расчет заклепочного соединения?

17. Что такое сварное соединение? Какие виды сварных соединений бывают?

18. Какие виды сварных швов применяются в сварных соединениях?

19. Как рассчитываются стыковые швы?

20. Как рассчитываются лобовые и фланговые швы?

ГЛАВА XI. ПЛОСКИЙ ИЗГИБ БРУСА

Общие сведения

Прямой брус, закрепленный с помощью опорных связей и нагруженный силами, которые вызывают его изгиб в одной плоскости, называется балкой. Балка является плоской и неподвижной системой. Форма и размеры поперечных сечений балки, как правило, одинаковые по всей длине. Такую балку называют балкой постоянной жесткости. Балка может быть статически определимой или статически неопределимой, в зависимости от количества опорных связей. Недвижимость балки в плоскости может быть обеспечена с помощью следующих видов опорных устройств.

а) Жесткое закрепление В (рис.11.1,а);

б) Шарнирно неподвижная опора С (рис.11.1,б и 11.1,в);

в) Шарнирно подвижная опора D (рис.11.1,б и 11.1,в).

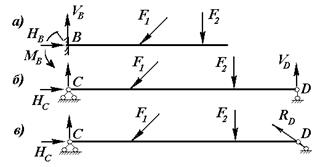
Рис. 11.1

Жесткое закрепление имеет три опорные связи и полностью обеспечивает недвижимость балки в плоскости, то есть не дает возможности балке перемещаться вдоль и перпендикулярно своей оси, а также исключает её поворот относительно опорной точки А. При нагрузке балки силами, произвольно расположенными в плоскости, в жесткой опоре возникают три составляющие реакции: вертикальная V_В, горизонтальная H_В, и опорный сосредоточенный момент М_В (рис.11.1,а). Если балка нагружена силами, которые действуют перпендикулярно оси, то горизонтальная реакция не возникает, то есть

H_В= 0 (рис.11.2,а).

Шарнирно неподвижная опора имеет две опорные связи, которые обеспечивают недвижимость балки вдоль своей оси и перпендикулярно к ней. Но эта опора не может удержать балку от ее поворота относительно своего центра. При произвольной нагрузке балки в плоскости в такой опоре возникают две составляющие реакции: вертикальная V_С и горизонтальная H_С (рис.11.1,б; 11.1,в и 11.2,в). Если балка нагружена силами, которые действуют перпендикулярно оси, то горизонтальная реакция не возникает, то есть H_С= 0 (рис. 11.2,б).

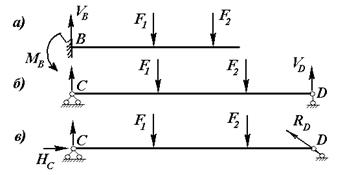
Рис.11.2

Шарнирно подвижная опора имеет одну опорную связь, то есть она обеспечивает недвижимость балки только в одном направлении. В вертикальном направлении, если эта опора расположена перпендикулярно оси балки, как показано на рис.11.1,б и 11.2,б, или в направлении опорного стержня, наклоненного под некоторым углом к оси балки (рис.11.1,в и 11.2,в). В такой опоре при произвольной нагрузке балки, возникает лишь одна реакция: вертикальная V_D (рис.11.1,в), или наклонна R_D, которая действует в направлении опорного стержня (рис. 11.2,в).

Неподвижность балки в плоскости можно обеспечить с помощью одной жесткой опоры, или двух шарнирных опор, одна из которых шарнирно неподвижна, а другая - шарнирно подвижна. В этом случае балка будет статически определимой и реакции опор определяются из уравнений равновесия статики.

Если нагрузка балки действует в одной плоскости, которая проходит через ось балки и содержит одну из главных осей инерции поперечного сечения этой балки, то ее деформирование происходит в этой плоскости и носит название плоского изгиба.

С целью упрощение расчета балки при определении внутренних усилий, действительную балку заменяют условно упругой материальной линией, которая совпадает с её осью. Эта линия закрепляется опорами и нагружается внешними силами. В таком виде она называется расчетной схемой балки. На рис. 11.1 и 11.2 показанные расчетные схемы некоторых балок. В следующих параграфах мы будем рассматривать расчетные схемы балки и иметь в виду, что поперечные сечения имеют заданную форму и размеры, которые устанавливаются соответствующими расчетами.

Расчетную схему в дальнейшем будем называть просто балкой.