Механические характеристики материалов
Рассматривая простой вид деформации стержня, растяжение или сжатие, мы установили, что в произвольном поперечном сечении стержня возникают продольная сила и нормальные напряжения. От действия этих сил стержень удлиняется или укорачивается на величину 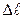 . При этом размеры поперечного сечения стержня соответственно уменьшаются, или увеличиваются.
. При этом размеры поперечного сечения стержня соответственно уменьшаются, или увеличиваются.
После определения продольных сил, нормальных напряжений, абсолютных и относительных деформаций возникает вопрос, будет ли обеспечена работоспособность стержня от действия внешних сил? Для этого необходимо установить допустимый уровень напряжений и деформаций стержня. Понятно, что допустимый уровень напряжений и деформаций зависит от материала, из которого изготовлен стержень и определяется экспериментальным путем. Для этого проводят испытание специальных образцов, изготовленных из того же материала, что и стержень сооружения. Испытание образцов осуществляют на испытательных машинах, которые позволяют увеличивать постепенно нагрузку от нуля до конечного значения, при котором наступает разрушение образца. Специальное устройство испытательных машин начерчивает график изменения деформаций при нагружении образца. Этот график называют диаграммой растяжения (сжатия) и используют для определения механических характеристик материалов.
Как правило, механические характеристики материалов определяются при испытании образцов на растяжение или сжатие. Образцы пластичных материалов изготовляют круглого или прямоугольного поперечного сечения.
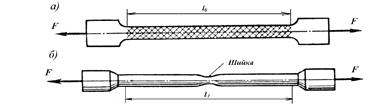
Рис. 9.11
Размеры поперечного сечения принимаются в зависимости от мощности испытательной машины. При этом отношение рабочей длины образца к размеру поперечного сечения принимается в пределах 6-10. На рис.9.11 показан эскиз стального образца, до испытания на растяжение и после его разрушения.
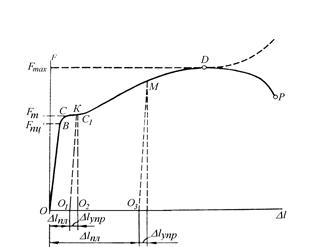
Рис.9.12
На образец наносят две метки, расстояние между которыми называют рабочей длиной 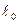 . При испытании образца устанавливается зависимость между силой его нагружения F и его абсолютным удлинением
. При испытании образца устанавливается зависимость между силой его нагружения F и его абсолютным удлинением 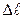 . Эта зависимость (диаграмма растяжения) начерчивается специальным устройством машины при испытании образца на растяжение. Она имеет вид, представленный на рисунке 9.12.
. Эта зависимость (диаграмма растяжения) начерчивается специальным устройством машины при испытании образца на растяжение. Она имеет вид, представленный на рисунке 9.12.
Анализируя диаграмму легко заметить, что сначала деформации образца остаются пропорциональными силе F до достижения ею некоторого значения Fпц (точка В на диаграмме).
При этом напряжение в поперечном сечении образца определяется за известной по формуле:
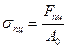 ,
,
и называется пределом пропорциональности.
Если напряжения не превышают величины 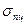 , стержень получает только упругие деформации, которые согласно закону Гука пропорциональны напряжениям. Если при достижении силой F величины Fпц остановить испытательную машину и разгрузить образец, то он полностью восстановит свои первоначальные размеры, то есть деформации (удлинение) полностью исчезнут. Как известно такие деформации являются упругими. Величину напряжения, при котором не возникают остаточные деформации, называют пределом упругости
, стержень получает только упругие деформации, которые согласно закону Гука пропорциональны напряжениям. Если при достижении силой F величины Fпц остановить испытательную машину и разгрузить образец, то он полностью восстановит свои первоначальные размеры, то есть деформации (удлинение) полностью исчезнут. Как известно такие деформации являются упругими. Величину напряжения, при котором не возникают остаточные деформации, называют пределом упругости
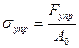 .
.
Предел упругости отвечает точке В1 диаграммы и практически совпадает с пределом пропорциональности.
При увеличении силы F от величины Fпц деформации образца будут увеличиваться интенсивнее, на диаграмме появляется криволинейный участок ВС, а при достижении силой F значения Fт деформации резко увеличиваются без изменения силы.
Участок СС1, диаграммы называется участком текучести, а напряжение, которое отвечает этому участку, называется пределом текучести:
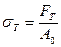 .
.
Если разгрузить образец от точки К диаграммы, то график разгрузки будет прямолинейным и параллельным упругому участку диаграммы. Прямая разгрузки КО1 параллельная прямой первой нагрузки образца ОВ. При этом общее удлинение ОО2 будет равняться сумме удлинений ОО1 и О1О2. Вторая часть общего удлинения О1О2 является упругой и исчезает при разгрузке образца, а первая часть ОО1 является остаточной и не исчезает, то есть длина образца увеличивается на эту величину.
При повторной загрузке образца график зависимости 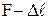 изменяется по прямой О1К и как видно из рис.9.12 предел пропорциональности и упругости увеличивается до величины, соответствующей точке К диаграммы, то есть возникает явление, которое называется упрочнением стали. При этом участок текучести уменьшается (КС1 вместо СС1). При дальнейшем увеличении нагрузки текучесть стали прекращается, и образец вновь обретает способность воспринимать нарастающие нагрузки до некоторого значения Fmax (точка D на диаграмме). Диаграмма ограничивается криволинейным участком С1D.
изменяется по прямой О1К и как видно из рис.9.12 предел пропорциональности и упругости увеличивается до величины, соответствующей точке К диаграммы, то есть возникает явление, которое называется упрочнением стали. При этом участок текучести уменьшается (КС1 вместо СС1). При дальнейшем увеличении нагрузки текучесть стали прекращается, и образец вновь обретает способность воспринимать нарастающие нагрузки до некоторого значения Fmax (точка D на диаграмме). Диаграмма ограничивается криволинейным участком С1D.
Напряжения, равное отношению наибольшей силы Fmax, которую может выдержать образец, к первоначальной площади поперечного сечения, имеет название предела прочности:
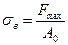 .
.
Если разгрузить образец от точки М диаграммы, то графиком разгрузки будет прямая МО3 // ОВ. При этом остаточная деформация увеличится до величины 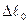 (отрезок ОО3).
(отрезок ОО3).
До достижения силой F значения Fmax размеры поперечного сечения образца изменяются медленно и равномерно по рабочей длины 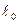 образца, согласно зависимости Пуассона. При достижении значения Fmax в некотором сечении образца возникает резкое уменьшение его размеров, то есть образуется так называемая шейка. Продольные и поперечные деформации образца увеличиваются при уменьшении величины нагрузки. График имеет криволинейный участок DЕ. Разрушение образца наступает при значении Fр значительно меньшем от Fmax. Это объясняется тем, что площадь поперечного разреза образца уменьшается от А0 до Ар.
образца, согласно зависимости Пуассона. При достижении значения Fmax в некотором сечении образца возникает резкое уменьшение его размеров, то есть образуется так называемая шейка. Продольные и поперечные деформации образца увеличиваются при уменьшении величины нагрузки. График имеет криволинейный участок DЕ. Разрушение образца наступает при значении Fр значительно меньшем от Fmax. Это объясняется тем, что площадь поперечного разреза образца уменьшается от А0 до Ар.
После разрушения образца, две его части соединяют и измеряют рабочую длину 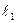 и диаметр сечения d1 после разрушения образца.
и диаметр сечения d1 после разрушения образца.
Эти значения позволяют определить следующие характеристики материала:
§ 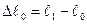 - абсолютную продольную деформацию при разрушении;
- абсолютную продольную деформацию при разрушении;
§ 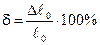 - относительную продольную деформацию после разрушения;
- относительную продольную деформацию после разрушения;
§ 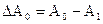 - абсолютное уменьшение площади поперечного сечения образца;
- абсолютное уменьшение площади поперечного сечения образца;
§ 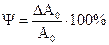 - относительное сужение образца при его разрушении.
- относительное сужение образца при его разрушении.
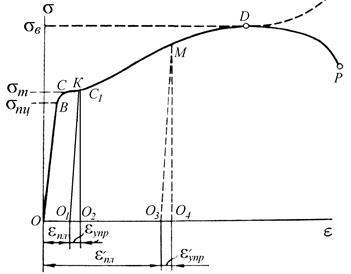
Рис. 9.13
Характеристики 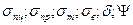 - являются основными механическими и пластичными характеристиками материалов, которые определяются в процессе испытания образцов. Для удобства определения механических характеристик материалов целесообразно построить диаграмму напряжений (рис. 9.13), которая подобна диаграмме растяжения. Если ординаты диаграммы растяжения разделить на начальную площадь поперечного сечения образца А0, а абсциссы этой диаграммы разделить на начальную длину образца
- являются основными механическими и пластичными характеристиками материалов, которые определяются в процессе испытания образцов. Для удобства определения механических характеристик материалов целесообразно построить диаграмму напряжений (рис. 9.13), которая подобна диаграмме растяжения. Если ординаты диаграммы растяжения разделить на начальную площадь поперечного сечения образца А0, а абсциссы этой диаграммы разделить на начальную длину образца 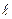 0, то получим соответствующую диаграмму напряжений.
0, то получим соответствующую диаграмму напряжений.
Эта диаграмма позволяет определить модуль продольной упругости материала E. Он равняется тангенсу угла наклона прямолинейного участка диаграммы к горизонтальной оси ε.
Некоторые пластичные материалы не имеют на диаграмме напряжений участка текучести (рис. 9.14). Для таких материалов вводится понятие условного предела текучести. За условную величину предела текучести принимается напряжение, которое соответствует остаточной деформации 0,2%. Эта условная величина обозначается σ0,2.
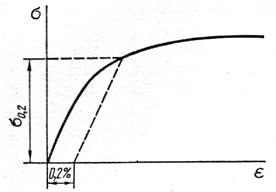
Рис.9.14
Механические характеристики хрупких материалов определяются при испытании образцов на растяжение и на сжатие. Например, для очень хрупкого материала, каким является серый чугун, испытание на растяжения и на сжатие дает возможность установить, что граница прочности при сжатии (кривая I на рис.9.15,а) значительно превышает границу прочности при растяжении (кривая II на рис.9.15,а).
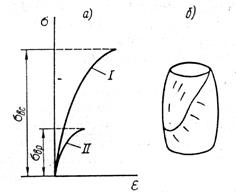
Рис. 9.15
При этом на диаграмме отсутствует прямолинейный участок (участок текучести) , а относительные деформации имеют значительно меньшие значения, чем для пластичных материалов. При испытании хрупких материалов на сжатие используют образцы в виде цилиндров (рис.9.15,б), или кубов. Образцы в виде кубов используют для определения характеристик каменных и бетонных изделий. Анализ разрушенных образцов при сжатии дает возможность выявить, что их разрушение происходит в плоскостях, наклоненных под углом 450 к оси образца, то есть в плоскостях, где действуют максимальные касательные напряжения.
Заметим, что механические характеристики материалов не являются постоянными величинами. Они зависит от многих условий, самыми главными из которых являются разные технологические факторы (технология изготовления, термическая и механическая обработка и тому подобное) и условия эксплуатации (среда, температура, характер нагрузки – статические или динамические и тому подобное).
Все механические и пластичные характеристики материалов очень существенно зависят от температуры. На рис.9.16,а начерченные графики изменения предела текучести и предела прочности, а также относительного удлинения δпосле разрушения образца из углеродистой стали. Как видно из этих графиков, в интервале температур 150 - 200°С предел прочности и предел текучести растут до максимальных значений, а относительное удлинение уменьшается до минимального значения.
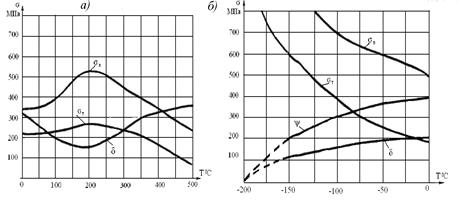
Рис. 9.16
При низких температурах пределы текучести и прочности углеродных сталей растут, но одновременно резко уменьшаются характеристики пластичности 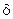 и
и 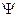 , что видно с рис.9.16,б. То есть материалы, которые при нормальной температуре являются пластичными, при низких температурах становятся хрупкими. Это явление имеет название хладноломкость. Но для таких материалов как алюминий, медь, никель хладноломкость не наступает, потому что при низких температурах наблюдается увеличение, как прочности, так и пластичных характеристик
, что видно с рис.9.16,б. То есть материалы, которые при нормальной температуре являются пластичными, при низких температурах становятся хрупкими. Это явление имеет название хладноломкость. Но для таких материалов как алюминий, медь, никель хладноломкость не наступает, потому что при низких температурах наблюдается увеличение, как прочности, так и пластичных характеристик 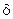 и
и 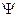 .
.
Дата добавления: 2018-11-26; просмотров: 1213;











