Теорема Котельникова.

Разложение непрерывных сигналов в ряд Котельникова

Телекоммуникационные сигналы делятся на непрерывные и дискретные.

Непрерывные сигналы (функции) могут принимать любые , сколь угодно близкие друг к другу значения, в любые моменты времени. Примером непрерывного сигнала является гармоническое колебание.

Дискретные (цифровые) сигналы могут принимать только заранее известные значения, отличающиеся одно от другого на конечную величину, причем изменяться эти значения могут только в определенные моменты времени. Примером дискретного сигнала является (см. рис.2.1 ) периодическая последовательность прямоугольных импульсов, которая в моменты времени ( -t/2 +кТ ) принимает значения или 0, или А.

Любая непрерывная функция, спектр которой не содержит частот

выше 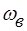, полностью определяется своими отсчетами, взятыми через интервал времени 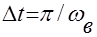. (Теорема Котельникова)

Временные диаграммы непрерывного сигнала x(t) и дискретизированного x _д(t) имеют вид:

x(t)

t

Dt 2Dt 3Dt 4Dt Рис. 3.1

x_д(t)

0 Dt 2Dt 3Dt 4Dtt

Важно, что не надо передавать непрерывно исходный сигнал x(t),

достаточно передавать отсчёты x(kDt). Это первый шаг перехода от

непрерывного сигнала к цифровому. С точки зрения математики теорема Котельникова означает представление сигнала в виде ряда:

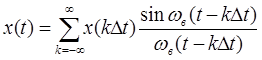(3.1)

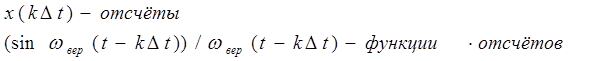Ряд Котельникова – это разложение сигнала 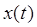в ряд по ортого-

нальным функциям .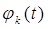

(3.2)

Теоретически дискретизация осуществляется с помощью d-импульсов . Временная диаграмма одиночного d- импульса имеет вид:

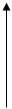u(t)

d(t-a)

Рис. 3.2 0 a t

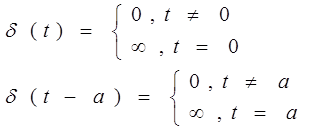
Спектр одиночного 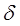- импульса получим, используя преобразование Фурье:

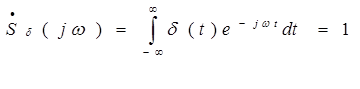
Использовано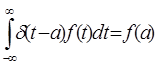
"фильтрующее" свойство дельта-функций:

Следовательно, спектр одиночного дельта-импульса имеет вид:

S(jw)

Рис. 3.3

w

Чтобы получить отсчёты функции 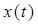перемножим функцию 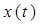на периодическую последовательность 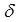- импульсов с периодом Т=Dt. Временная диаграмма периодической последовательности дельта-импульсов имеет вид:

u_d(t)

d(t+4Dt) d(t+3Dt) d(t+2Dt) d(t+Dt) d(t) d(t-Dt) d(t-2Dt) d(t-3Dt)

. . . . . . .

-4Dt -3Dt -2Dt -Dt 0 Dt 2Dt 3Dt 4Dt t

Рис.3.4

Так как сигнал периодический, то его спектр будет дискретным.

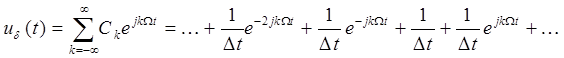
(3.3)

;

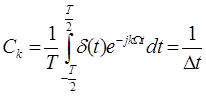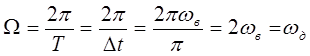
Т =D t ; 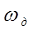-частота дискретизации.

Спектр периодической последовательности 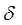- импульсов в соответствии с формулой для U(t) имеет следующий вид :

S(jw)

1/Dt Рис.3.5

. . . . . . . . . . .

t

--3w_д -2w_д -w_д 0 w_д 2w_д 3 w_д w