Непрерывных сигналов.
Теорема Котельникова точно справедлива только для сигналов с финитным (конечным) спектром. На рис.3.14 показаны некоторые варианты финитных спектров:
 Sx(w) 3
Sx(w) 3
 2
2

 1
1
 0 wв w
0 wв w
Рис.3.14.
Однако спектры реальных информационных сигналов бесконечны. В этом случае теорема Котельникова справедлива с погрешностью.
 Sx(w)
Sx(w)


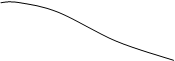
0 wв w
Рис.3.15.
Погрешность дискретизации определяется энергией спектральных составляющих сигнала, лежащих за пределами частоты wв.
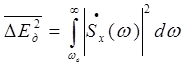 (3.7)
(3.7)
Вторая причина возникновения погрешностей - неидеальность восстанавливающего ФНЧ.
Т.о. погрешность дискретизации и восстановления непрерывного сигнала определяется следующими причинами:
1) Спектры реальных сигналов не финитны.
2) АЧХ реальных ФНЧ неидеальны.
Например, если в качестве ФНЧ использовать RC- фильтр, то восстановленный сигнал на его выходе будет иметь вид:
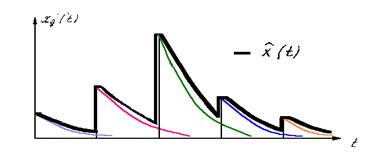
Рис.3.16.

с учетом того, что импульсная реакция RC-фильтра равна: 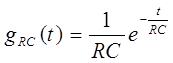
Вывод: чем выше 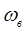 и чем ближе характеристики ФНЧ к идеальным, тем ближе восстановленный сигнал к исходному.
и чем ближе характеристики ФНЧ к идеальным, тем ближе восстановленный сигнал к исходному.
Вопросы для самопроверки.
1. Какие сигналы называются непрерывными?
2.Какие сигналы называются дискретными?
3. Сформулируйте теорему Котельникова.
4.Рассчитайте и постройте спектр дискретизированного сигнала.
5. Рассчитайте и постройте спектр сигнала АИМ.
6. Как восстановить непрерывный сигнал из отсчетов?
7. Чем определяются погрешности дискретизации и восстановления сигналов?
Дата добавления: 2016-06-22; просмотров: 1864;











