Спектр дискретизированного сигнала.

Рассмотрим временные диаграммы исходного и дискретизированного сигналов:

x(t)

t

Dt 2Dt 3Dt 4Dt Рис. 3.6

x_д(t)

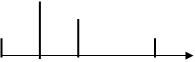0 Dt 2Dt 3Dt 4Dtt

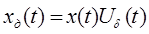-дискретизированный сигнал

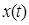- исходный сигнал.

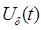-периодическая последовательность 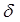- импульсов

Разложим периодическую последовательность d-импульсов в ряд Фурье, как мы это делали выше:

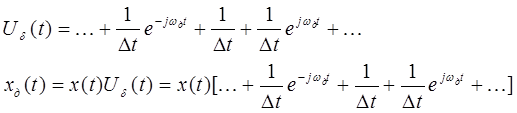
Найдём спектр дискретизированного сигнала.

(3.4)

Т.о. мы видим, что спектр дискретизированного сигнала содержит спектр исходного сигнала S_x(w), спектр исходного сигнала смещенный на величину частоты дискретизации вправо S_x(w - w_д), тот же спектр смещенный на величину частоты дискретизации влево S_x(w+ w_д), тот же спектр смещенный на величину 2w_д и т.д.

Спектр исходного непрерывного сигнала.

S_x(w)

Рис.3.8

-w_g w_g w

Спектр дискретизированного сигнала : _·

S_д(w)

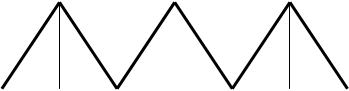Рис.3.9

……….. …………

(-w_д - w_в) - w _д - w_в 0 w_в w_д (w_д + w_в) w

3.3. Спектр дискретизированного сигнала при дискретизации импульсами конечной длительности (сигнал амплитудно-импульсной модуляции или АИМ сигнал).

Очевидно, что реально мы располагаем не последовательностью дельта-импульсов, а последовательностью импульсов конечной длительности.

В результате процесса дискретизации мы получим не последовательность дельта-импульсов, амплитуда которых соответствует значению непрерывного сигнала в тактовые моменты времени, а последовательность реальных, например, прямоугольных импульсов, амплитуда которых соответствует значениям непрерывного сингнала в тактовые моменты времени.

Рассмотрим временные диаграммы :

x(t) аналоговый сигнал

t

U(t) периодическая последовательность импульсов

t

x_аим(t) сигнал АИМ

t

0 Dt 2Dt 3Dt 4Dt ……

Рис.3.10.

АИМ сигнал можно записать в виде:

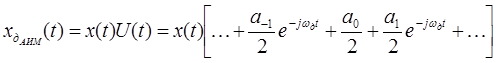
U(t)-периодическая последовательность импульсов.

В квадратных скобках – ряд Фурье для последовательности импульсов конечной длительности.

Спектр АИМ сигнала,следовательно, похож на спектр дискретизированного сигнала при дискретизации дельта -импульсами , но амплитуда составляющих спектра убывает с ростом номера гармоники : 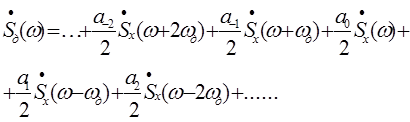(3.5)

Спектр АИМ сигнала в соответствии с формулой (3.5) принимает вид, показанный на рис.3.11.

_·

S_д(w)

-2w_д - w _д - w_в 0 w_в w_д 2w_д w

Рис.3.11