Демодулятор – преобразует ВЧ модулированный сигнал в НЧ модулирующий ( сигнал на выходе демодулятора, примерно,
Соответствует тому, что было на входе модулятора).
Декодер – а) принимает решение по каждой посылке(1 или 0),
Б) декодирует кодовые комбинации , исправляет часть
Ошибок,
Г) преобразует кодовые комбинации в сообщения удобные
Для получателя.
Получатель сообщения - человек, компьютер или другие технические устройства.
Входное устройство, демодулятор и декодер образуют приемник.
КОДЕР + ДЕКОДЕР = КОДЕК
МОДУЛЯТОР + ДЕМОДУЛЯТОР = МОДЕМ
КОДЕР+МОДУЛЯТОР+ДЕКОДЕР+ДЕМОДУЛЯТОР=КОДЕМ
Вопросы для самопроверки.
1. Какие блоки входят в состав обобщенной структурной схемы системы связи?
2. Какие блоки входят в состав передатчика?
Какие блоки входят в состав приемника?
4. Укажите назначение основных блоков структурной схемы?
Разложение сигналов в ряд по ортогональным
Функциям.
Общие положения
Для исследования различных свойств сообщений, сигналов и помех удобно использовать разложение этих процессов в ряды.
Любой процесс (с некоторыми математическими ограничениями ) можно представить в виде ряда:
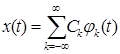 jk(t) - ортогональные функции, т.е.:
jk(t) - ортогональные функции, т.е.:  (2.1)
(2.1) 

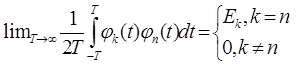

 Ck - коэффициенты разложения, Еk - энергия ортогональных функций.
Ck - коэффициенты разложения, Еk - энергия ортогональных функций.
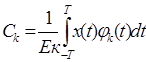
2.2. Ряд Фурье.
Если выбрать в качестве ортогональных функций:
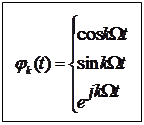
то этот ряд (2.1) называется рядом Фурье.
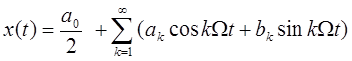
 (2.2)
(2.2)
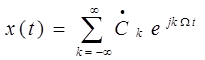 ;
; 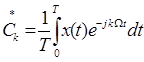
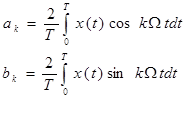
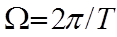
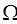 - частота первой гармоники, определяемая периодом T
- частота первой гармоники, определяемая периодом T
( T- период функции x(t) ).
Разложение сигнала в ряд Фурье называется спектром сигнала.
Спектр периодического сигнала – дискретный.
Спектр непрерывного сигнала – сплошной и определяется интег-
ралом Фурье: -¥
S(jw) = ò x(t)e -jwt dt (2.3)
- ¥
Шириной спектра сигнала Пэназывается полоса частот, в пределах которой заключена основная доля энергии сигнала.
В качестве примера рассчитаем спектр периодической последовательности прямоугольных импульсов c амплитудой А:
 x(t)
x(t)


 А
А
. . . .Рис.2.1






 t T t
t T t
Определим коэффициенты разложения в ряд Фурье Cк :
 | 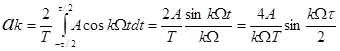 | ||
t/2
bk = 2/Т ò A sin kWt dt = 0, т.к. подинтегральная функция - нечетная.
-t/2
Пусть Т = 2t, тогда коэффициенты ak равны:
a0 = А, ak = 2А/ kp (sin kp/2), при к > 0.
Итак, временная диаграмма периодической последовательности импульсов показана на рис.2.1. Спектр этой последовательности показан на рис.2.2.
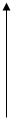 ak
ak
 2A/p
2A/p

 A/2
A/2
2A/3p Рис.2.2.

 . .
. .
0 W 2W 3W 4W w
Ширина спектра сигнала равна, в данном случае, Пэ =2p/t.
Спектр непериодического сигнала ( спектральная плотность) , как уже сказано выше, может быть получен с помощью интеграла Фурье. Для одиночного прямоугольного импульса с амплитудой А и длительностью t на рис.2.3 получим спектр S(jw) на рис.2.4 :
 |
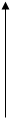 S(jw)
S(jw)
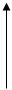
 x(t)
x(t)
 А
А








 t t 0 w
t t 0 w
2p/t 4p/t
Рис.2.3. Рис.2.4.
Спектр непериодического сигнала сплошной, бесконечный, ширина спектра определяется длительностью сигнала и, ориентировочно, равна Пэ =2p/t.
Вопросы для самопроверки
1. Какие функции называются ортогональными?
2. Запишите ряд Фурье в общем виде.
3. Что такое спектр сигнала?
4. Запишите выражение для спектра периодического сигнала.
5. Рассчитайте амплитуды гармонических составляющих для периодической последовательности прямоугольных импульсов.
6. Что такое ширина спектра сигнала?
7. Чему равна ширина спектра последовательности импульсов?
8. Запишите выражение для спектра непериодического сигнала.
9. Рассчитайте и постройте спектр одиночного прямоугольного импульса.
10. Какие параметры сигнала влияют на ширину спектра и на частоту гармонических составляющих спектра?
Дата добавления: 2016-06-22; просмотров: 2068;











