Статический момент площади относительно оси и его использование для определения координат центра тяжести плоской фигуры

Плоскую фигуру, ограниченную замкнутым контуром произвольного очертания, можно рассматривать как однородное тело весьма малой и постоянной толщины. Такое тело называют в механике пластинкой. На рис.6.13 изображена пластинка произвольной формы, совмещенная с плоскостью этого рисунка. Обозначим площадь пластинки буквой A , а её толщину - буквой h. Отнесем пластинку к прямоугольной сис­теме координат Оyzиразобьем её на конечное число площадок. Рассмотрим одну из них, взятую в окрестности точки В_i и имеющую площадь A_i.

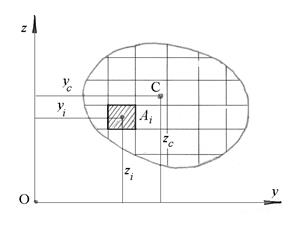
Рис.6.13

Объем 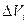этой части пластинки определится произведением её площади A_i на толщину h пластинки, т.е: 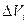=A_i∙h

Для получения полного объема пластинки необходимо взять сумму всех элементарных объемов:

(6.23)

Подставляя в две последние формулы (6.22) вместо 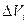и V их значения, и сокращая на h, , получим:

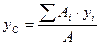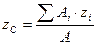, (6.24)

Произведение элементарной площадки A_i на расстояние её центра тяжести до некоторой оси называется статическим моментом этой площадки относительно оси. Пользуясь этим определением можно запи­сать выражения статических моментов площади A_i.относительно осей y и z:

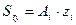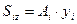, (6.25)

Алгебраическая сумма произведений элементарных площадок на расстояния их центров тяжести до некоторой оси называется стати­ческим моментом площади всей плоской фигуры относительно той же оси, т.е:

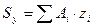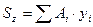, (6.26)

При использовании выражений (6.26) формулы (6.24) для координат центра тяжести плоской фигуры принимают вид:

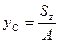, (6.27)

Статические моменты плоской фигуры относительно осей, прохо­дящих через её центр тяжести равны нулю. Положим, что ось y про­ходит через центр тяжести. Тогда z_c = 0 и из второй формулы (6.27) следует, что статический момент всей площади относительно оси y равен нулю, т.е: 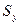= 0 . Аналогично 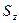= 0, если ось z проходит через центр тяжести плоской фигуры.