Центр тяжести твердого тела

Всякое тело, расположенное в сфере земного притяжения обладает весом, т.е. на тело в целом и на каждую его частицу действует сила тяжести, направленная к центру Земли. Так как в механике рассмат­риваются малые тела по сравнению с расстоянием их до центра Земли, то все силы тяжести, действующие на элементарные частицы тела, образуют систему параллельных сил.

Пусть задано тело произвольной формы и известны силы 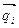, дей­ствующие на каждую его элементарную частицу тела. Линии действия указанных сил параллельны между собой (рис.6.12). Сложив силы тя­жести всех элементарных частиц тела, получим их равнодействующую 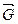, называемую силой тяжести всего тела или его весом. Модуль силы тяжести равен алгебраической сумме модулей всех элементарных сил 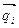, т. е:

.

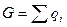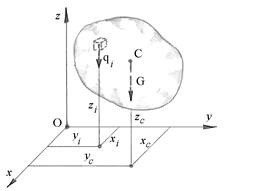
Рис.6.12

Точка С, в которой приложена сила тяжести тела, называется его центром тяжести. На основании свойства точки С, указанного в предыдущем параграфе, её положение в теле не зависит от ориента­ции этого тела в пространстве.

Формулы для определения центра тяжести тела в любом его поло­жении, вытекают из выражений (6.20) при замене в них внешних сил 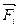силами тяжести 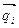. В результате получим:

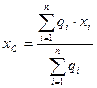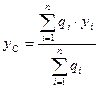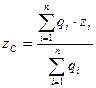, , (6.21)

Для однородных тел, объем которых заполнен одним и тем же ве­ществом, формулы (6.21) могут быть приведены к более удобному виду. Обозначим объемный вес тела через γ . Тогда сила тяжести любой элементарной частицы, имеющей объем 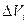будет равна q_i = γ∙ 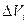а сила тяжести всего тела определится выражением:

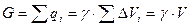
где V - полный объем тела.

После подстановки в зависимости (6.21) вместо G и q_i их зна­чений и после сокращения γ в числителях и знаменателях получен­ных равенств, найдем:

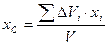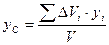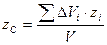, , (6.22)

Здесь 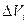- элементарные или конечные объемы рассматриваемого те­ла с известными координатами их центров тяжести х_i,у_i, z_i.