Система параллельных сил в пространстве. Условия и уравнения равновесия

Результаты приведения произвольно расположенных сил в прост­ранстве к заданному центру, полученные в § 6.3., распространяются и на случай параллельных сил. При этом достигается сокращение условий и уравнений равновесия.

Положим, что в точках А, В, С,...К твердого тела действуют силы 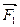, , 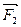,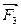…, , 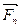направленные вдоль параллельных прямых в разные стороны (рис.6.7).

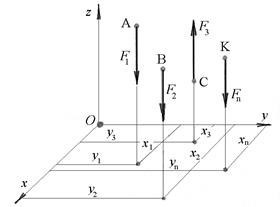
Рис.6.7

Отнесем рассматриваемые силы к прямоугольной системе координат с началом в некоторой точке О - центре приведения, и одну ось, например ось z , направим параллельно силам. Тогда проекции каждой силы на координатные оси х и y будут равны нулю тождественно. Так как заданные силы параллельны оси z, то момент каждой из них относительно этой оси равен нулю, т.е. алгебраичес­кая сумма моментов всех сил относительно оси В тождественно рав­на нулю.

В результате устанавливаем, что для равновесия системы параллельных сил необходимо и достаточно выполнить следующие три усло­вия:

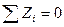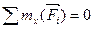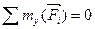, , (6.13)

Итак, для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы одновременно были равными нулю алгебраическая сумма проекций всех сил на параллельную им ось и алгебраические суммы моментов всех сил относительно каждой из двух осей х и y, лежащих в плоскости, перпендикулярной линиям дейст­вия заданных сил.