Из логарифмов констант равновесия реакций образования некоторых веществ.
Таблица содержит lgKaf образования соединений из простых веществ для температур от 500 до 1000 К с шагом в 100 К.
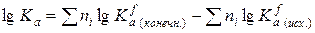
Примеры решения задач
Задачи на вычисление состава равновесной смеси подробно рассмотрены в теоретических пояснениях (страница 32).
Задача 1.
Константа равновесия реакции Н2 +СI2 = 2 НС1
при 1000 К равна 2,67·1010. При этой температуре и давлении 1 атм степень диссоциации водяного пара равна 2,52·10-7 . Определить константу равновесия реакции
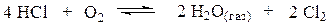
Решение:
Определяем константу равновесия искомой реакции из значения DG0 для этой реакции, которое найдем методом комбинирования
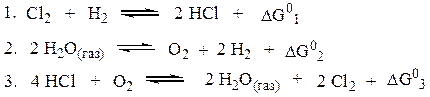
| ∙ (-2) ∙ (-1) |
Комбинируя уравнения 1 и 2 надо получить уравнение 3. Для этого первое уравнение умножим на (-2), а второе на (-1). После чего сложим левые и правые части полученных уравнений. Видим, что полученное уравнение аналогично уравнению 3:
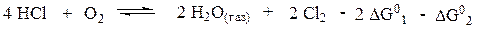
Таким образом, DG°3 = -2 DG°1 - DG°2
По уравнению нормального сродства 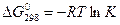
- 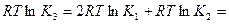 >
> 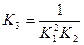
Значение К1, дано в условии задачи, а К2 можно найти по степени диссоциации (смотри теоретические пояснения)
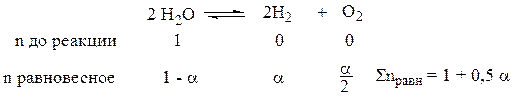
Δn = 3 – 2 = 1
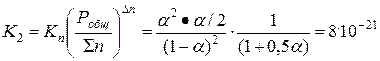
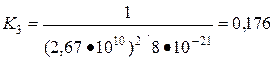
Задача 2.
Константа равновесия реакции  при 360o C равна 0,015, а при 444 °С равна 0,020. Найти среднее значение теплового эффекта реакции в этом интервале температур и рассчитать константу равновесия при 400 °С.
при 360o C равна 0,015, а при 444 °С равна 0,020. Найти среднее значение теплового эффекта реакции в этом интервале температур и рассчитать константу равновесия при 400 °С.
Дано:
t1 = 360 0C, T1 = 633 K
t2 = 444 0C, T2 = 717 K
t3 = 400 0C, T3 = 673 K
K1 = 0,015; К2 = 0,020
DН = ?
К3 = ?
Решение:
Интегрирование уравнения изобары при ΔН=const дает уравнение (1.27, стр. 37):
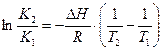 , откуда
, откуда
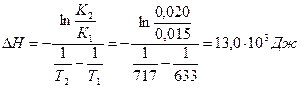
По этому же уравнению находим К3, используя найденное значение DН:
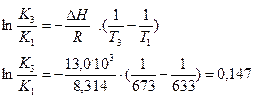
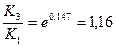
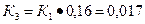
Задача 3.
Определить тепловой эффект реакции:
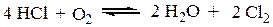
при 1000 К, если известна зависимость lgK=f (T) для двух реакций:
1) Н2 + Сl2 = 2HCl
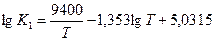
2) 2H2O = 2H2 + O2
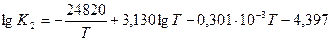
Решение
Сложная зависимость lgK=f (T) (нелинейная) говорит о зависимости теплового эффекта реакции от температуры.
Для нахождения ΔН используем уравнение изобары Вант Гоффа:
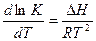 ; откуда
; откуда 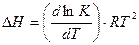 .
.
Зависимость lnK = f(T) искомой реакции найдем методом комбинирования, воспользовавшись данными, полученными в задаче 1, где рассматривается эта же реакция.
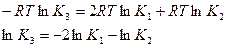
Используем соотношение lnK=2,3lgK
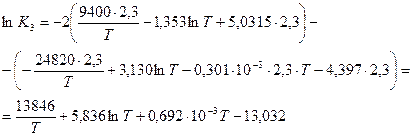
ФАЗОВЫЕ РАВНОВЕСИЯ
Основные понятия и определения
Фаза - совокупность однородных частей системы, обладающих в любом элементе объёма одинаковыми химическими и термодинамическими свойствами и отделенных от других однородных частей поверхностями раздела.
Системы, содержащие одну фазу называются гомогенными, две и более - гетерогенными.
Таблица 2.1 – Примеры различных систем
| Система | Фазы | Составные части | Компоненты |
| Н2О(тв)+Н2О(ж)+Н2О(г) | 1тв+1ж+1г = 3 | ||
| Р (белый) + Р (красный) | 2 тв. | ||
| Раствор(NaCl+KNО3+H2О)+NaС1тв | 1ж +1тв = 2 | ||
| Раствор (С6Н6+С6Н5СНз) | 1ж | ||
| С6Н6(ж)+Н20(ж) | 2ж |
Составная часть системы - химически индивидуальное вещество, которое можно выделить из системы и которое может устойчиво существовать вне её. Так в системе I составная часть одна; в системе 2 тоже одна (фосфор); в системе 3 можно выделить пять химически индивидуальных веществ: NaCl, KN03, NaN03, KCI, H20 - следовательно, здесь пять составных частей.
Независимые компоненты, или просто компоненты системы, - это химически индивидуальные вещества, наименьшее число которых достаточно для образования системы. Если в системе между составными частями нет химического взаимодействия, то число составных частей равно числу компонентов. Например, системы 4 и 5 имеют две составные части, два компонента. В системе 3 соли реагируют между собой по реакции:

и, следовательно, для составления системы 3, кроме Н20, достаточно взять три любые соли из четырех. Значит, эта система, имея пять составных частей, является четырехкомпонентной.
Число независимых компонентов равно разности между числом составных частей и числом химических реакций, протекающих между ними.
Термодинамические степени свободы - параметры системы, которые можно произвольно и независимо друг от друга менять, не вызывая изменения числа и природы фаз системы.
Число термодинамических степеней свободы (С), (так называемая вариантность системы) при равновесии связано с числом компонентов (К) и числом фаз (Ф ) закономерностью, которая называется правилом фаз Гиббса:
С = К - Ф + n. ,
где n- число внешних параметров; для однокомпонентной системы п = 2 (Р и Т), для двухкомпонентной системы n= 1 (Т, при Р = const). Если С = 0 -система инвариантна; С = 1 - моновариантна; С = 2 -дивариантна.
2.2 Однокомпонентные системы
В однокомпонентных системах могут быть одна, две или три устойчиво существующих фазы: твердая, жидкая, газообразная. Наибольший практический интерес представляют двухфазные равновесные системы.
Условием фазового равновесия системы является равенство химического потенциала в обеих фазах, μl = μll; μi = Gi0 следовательно, Gl = Gll
При изменении условий (Р, Т) система переходит из одного равновесного состояния в другое равновесное, при этом Gl и Gll изменяются на одну и ту же величину:
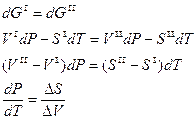
Поскольку при фазовом превращении:
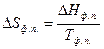 , то
, то 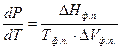 (2.1).
(2.1).
Это уравнение называется уравнением Клапейрона – Клаузиуса. Оно дает зависимость давления от температуры равновесной двухфазной системы. В форме (2.1) оно применимо к любому двухфазному равновесному превращению.
Пример диаграммы однокомпонентной системы приведен на рисунке 2.2. Проанализируем это уравнение применительно к двум типам фазовых равновесных превращений:
1 Равновесия между двумя конденсированными фазами.
Конденсированными – в отличие от газовой – называют обычно жидкие и кристаллические фазы. Между ними возможны равновесия: кристаллы  жидкость; кристаллы (α)
жидкость; кристаллы (α)  кристаллы (β)и т.п. Для фазового равновесия кристаллы
кристаллы (β)и т.п. Для фазового равновесия кристаллы 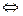 жидкость уравнение (2.1) имеет вид:
жидкость уравнение (2.1) имеет вид:
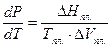 (2.2)
(2.2)
При плавлении теплота поглощается (ΔНпл.>0). Если Vж. > Vкр., то ΔVпл.> 0 и 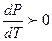 или
или 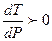 . Это значит, что увеличение давления вызывает повышение температуры плавления. Подавляющее большинство веществ подчиняются этой закономерности (кривая ОАl рисунок 2.1).
. Это значит, что увеличение давления вызывает повышение температуры плавления. Подавляющее большинство веществ подчиняются этой закономерности (кривая ОАl рисунок 2.1).
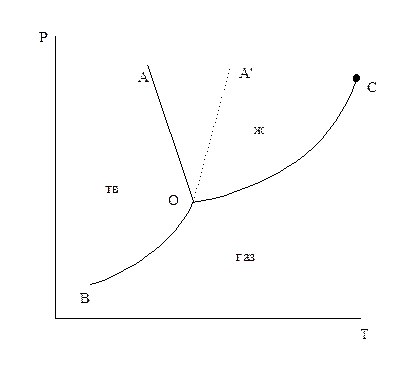
Рисунок 2.1 – Диаграмма состояния однокомпонентной системы
ОВ – кривая возгонки;
ОС – кривая кипения;
ОА – кривая плавления (для Н2О);
ОАl – плавление прочих веществ;
точка С – критическая точка;
точка 0 – тройная точка.
Однако, некоторые вещества, такие как вода, галлий, висмут, некоторые сорта чугуна характеризуются меньшей плотностью кристаллической решетки по сравнению с жидкой. Для них 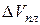 < 0 и
< 0 и 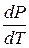 < 0, т.е. увеличение давления приводит к понижению температуры плавления (кривая ОА рисунок 2.1). Обычно ΔVпл. мало (5·10-6 - 15·10-6 м3/моль) и мало зависит от Р и Т, поэтому
< 0, т.е. увеличение давления приводит к понижению температуры плавления (кривая ОА рисунок 2.1). Обычно ΔVпл. мало (5·10-6 - 15·10-6 м3/моль) и мало зависит от Р и Т, поэтому  имеет большие значения. Так, для С6Н6 ≈ 350·105 Па/К; Н2О ≈ 130·105 Па/К; Sn ≈ 300·105 Па/К. Приняв, что в небольшом интервале температур
имеет большие значения. Так, для С6Н6 ≈ 350·105 Па/К; Н2О ≈ 130·105 Па/К; Sn ≈ 300·105 Па/К. Приняв, что в небольшом интервале температур 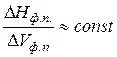 уравнение (2.1) можно проинтегрировать:
уравнение (2.1) можно проинтегрировать:
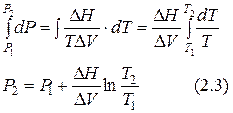
Это уравнение применимо только для равновесия между конденсированными фазами.
Дата добавления: 2016-06-22; просмотров: 2986;











