Равновесие между конденсированными и газообразными фазами

Это равновесие типа кристаллы пар; жидкость пар. Для этих фазовых равновесий всегда положительны, так как ΔН > 0 и ΔV > 0. Это значит, что нагревание системы всегда вызовет увеличение давления насыщенного пара, а повышение внешнего давления приведет к повышению температуры кипения (линии ОВ и ОС на рисунке 2.1).

Приведем уравнение 2.1 к виду более удобному для практического применения. Используем два приближения:

1. При температурах, далеких от критической, V_пар>>V_ж; V_пар>>V_тв.; ΔV ≈ V_пар.

2. Вдали от критической температуры насыщенный пар подчиняется уравнению состояния идеальных газов

,

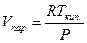Тогда уравнение (2.1) преобразуется следующим образом:

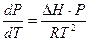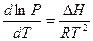, или (2.4)

Интегрирование этого уравнения при 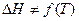дает линейную зависимость lnP от

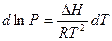
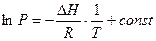(2.5)

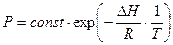
Рисунок 2.2 – зависимость давления насыщенного пара от температуры в координатах (ln P;1/Т)

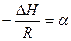- тангенс угла наклона прямой к оси абцисс:

,

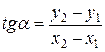где (y₂; х₂)_, (y₁; х₁) – координаты двух точек, лежащих на прямой.

Точки (не обязательно экспериментальные) выбирать отстоящими подальше друг от друга.

Коэффициент «b» из графика найти невозможно, если в начале координат не 0. Поэтому найти «b» можно из уравнения для какой-либо точки, лежащей на прямой. Определив «а», найти теплоту испарения:

ΔН = - Rtgα,

где R=8,31 Дж/моль·К.

Интегрирование уравнения в определенных пределах приводит к уравнению:

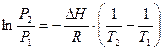(2.6)

по которому можно рассчитать теплоту испарения по двум экспериментальным значениям давлений и температур.

Согласно эмпирическому правилу Трутона молярная энтропия испарения при нормальной температуре кипения для многих жидкостей постоянна и равна:

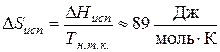
где Т_н.т.к. – нормальная температура кипения при Р = 1 атм.

Для полярных жидкостей с сильными межмолекулярными взаимодействиями ΔS_исп. превышает данную величину. Например, для воды она равна 109 .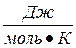

2.3 Примеры решения задач.

Задача 1

Зависимость температуры плавления нафталина от давления выражается уравнением: t_пл = 80,10 + 0,0371×10^-5P(Па) – 186,99×10^-18Р² (Па).

Рассчитать изменение объема при плавлении 1 кг нафталина при Р = 1 атм, если его теплота плавления равна 138,6 Дж/кг.

Дано:

m_нафт. = 1 кг

DН_пл. = 138,6 Дж/г

Р = 1 атм = 1,0133×10⁵ Па

DV_пл. - ?

Решение:

Для фазовых переходов конденсированных фаз применяется уравнение: .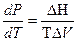

Определим сначала производную . Так как Т = t + 273,15; ;

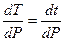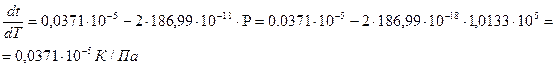
Откуда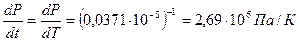

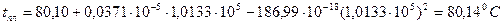
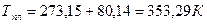
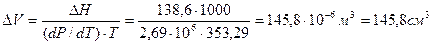
Задача 2

Давление пара хлороформа при 50 ⁰С равно 535 мм. рт. ст., теплота испарения хлороформа 30,836 кДж/моль. Определить нормальную температуру кипения хлороформа.

Дано:

T₁=50 ⁰C = 323 К

Р₁ = 535 мм. рт. ст.

Р₂ = 1 атм. = 760 мм.рт.ст.

DН_исп. = 30,836 кДж/моль

Т_{2 кип.} - ?

Решение:

Нормальная температура кипения (н.т.к.) – температура кипения при Р = 1 атм.

Для решения используется уравнение для фазового перехода с участием газов:

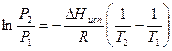
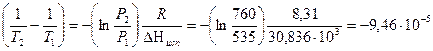
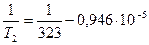
Т₂ = 333 К

Примечание. В данной задаче теплота испарения в данном температурном интервале принята постоянной, поэтому было использовано уравнение для DН = соnst.

Если же DН_исп. = f (Т), то надо использовать дифференциальное уравнение для нахождения DН_исп или DН_возг. Поскольку зависимости lnP=f(T) и lnK_P=f(T) аналогичны, предлагаем обратиться к решению задачи № 3 на странице 42.

2.4 Двухкомпонентные системы