Равновесие раствор – кристаллический компонент
Если два компонента А и В смешать, расплавить до получения однородного раствора, а затем начать охлаждать, то при некоторой температуре из раствора начнут образовываться кристаллы, так как растворимость веществ с понижением температуры, как правило, уменьшается. В зависимости от состава исходного раствора при понижении температуры он становится насыщенным по отношению либо к компоненту А, либо В, что приводит к кристаллизации соответственно А или В. В зависимости от состава раствора температура начала кристаллизации будет также различной. Иначе говоря, состав раствора, насыщенного каким-либо компонентом, т.е. растворимость этого компонента, зависит от температуры.
Уравнением, описывающим зависимость растворимости кристаллических веществ в жидкостях от температуры, является уравнение Шредера:
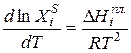 , (2.7)
, (2.7)
где 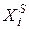 - молярная доля i-гo компонента в растворе, насыщенном по отношению к этому компоненту;
- молярная доля i-гo компонента в растворе, насыщенном по отношению к этому компоненту; 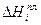 - теплота плавления этого компонента.
- теплота плавления этого компонента.
Уравнение Шредера справедливо только для идеальных растворов. Из анализа уравнения (2.7) следует, что растворимость твердых веществ в жидкостях растет с ростом температуры. Действительно, правая часть уравнения для идеальных растворов всегда больше нуля, следовательно, производная 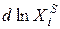 /
/ 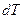 > 0, т.е. Xi растёт с ростом температуры.
> 0, т.е. Xi растёт с ростом температуры.
Интегрируя уравнение (2.7) для бинарной системы в пределах от Х1=1 (чистый компонент) до Х2 = Xs (насыщенный раствор при любой температуре), получим уравнение Шредера в интегральной форме:
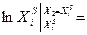 -
- 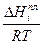
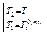

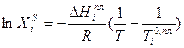
Пользуясь этим уравнением, можно найти растворимость i-гo компонента, выраженную в молярных долях Xi при любой температуре. Если раствор идеален и рассматривается во всём интервале концентраций от ХА = 1 до Хв = I, необходимо иметь в виду, что при одних составах раствор оказывается насыщенным компонентом А (здесь надо говорить о растворимости компонента А в В), при других - компонентом В (здесь уже идет речь о растворимости В в А). В первом случае применимо уравнение Шредера для компонента А; во втором – для компонента В:
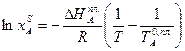 (2.8)
(2.8)
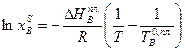 (2.9)
(2.9)
Очевидно, должен быть и такой раствор, который является насыщенным сразу обоими веществами, для него 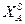 = 1 -
= 1 - 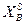 . Координаты такой системы Xs и Т находятся совместным решением уравнений 2.8 и 2.9 или графическим пересечением кривых, описываемых уравнениями 2.8 и 2.9. Кривые изменения растворимости компонентов А и В с температурой можно изобразить на одной диаграмме (рисунок 2.4).
. Координаты такой системы Xs и Т находятся совместным решением уравнений 2.8 и 2.9 или графическим пересечением кривых, описываемых уравнениями 2.8 и 2.9. Кривые изменения растворимости компонентов А и В с температурой можно изобразить на одной диаграмме (рисунок 2.4).
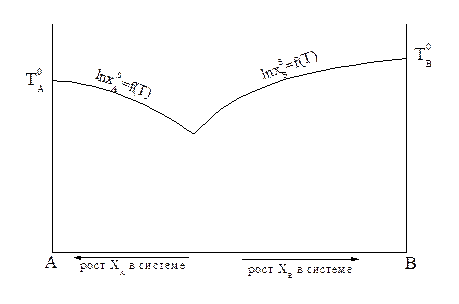
Рисунок 2.4 - Кривые зависимости растворимости компонентов А и В от температуры
Кривые охлаждения
Расчёт диаграмм растворимости (с равным правом их можно назвать диаграммами плавкости) возможен лишь для идеальных систем. Для реальных систем приходится экспериментально определять температуру, при которой раствор данной концентрации становится насыщенным. Это производится путем снятия так называемых кривых охлаждения для систем нескольких составов (метод называется термическим анализом), в координатах (температура; время).
При охлаждении однокомпонентной жидкости сначала происходит равномерное понижение температуры во времени. Появление кристаллов сопровождается выделением тепла, которое компенсирует теплоотвод, и дальнейшего понижения температуры в системе не происходит до полной кристаллизации жидкости, после чего температура снова понижается (рисунок 2.5 а).
Для двухкомпонентной системы наблюдается иной тип кривой охлаждения (рисунок 2.5 б). Сначала жидкая система охлаждается равномерно с определенной скоростью 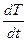 . Затем при какой-то температуре Т раствор становится насыщенным по отношению к какому-либо одному из компонентов, и этот компонент образует первые кристаллы. При данной температуре устанавливается равновесие между раствором и кристаллами. Дальнейшая кристаллизация этого компонента возможна лишь при понижении температуры. Таким образом, кристаллизация одного компонента из раствора происходит не при одной температуре, как в случае чистого вещества, а в некотором интервале температур. Поскольку кристаллизация вещества происходит небольшими порциями, то выделяющейся теплоты кристаллизации недостаточно для температурной остановки: происходит лишь уменьшение скорости охлаждения, кривая охлаждения становится более пологой.
. Затем при какой-то температуре Т раствор становится насыщенным по отношению к какому-либо одному из компонентов, и этот компонент образует первые кристаллы. При данной температуре устанавливается равновесие между раствором и кристаллами. Дальнейшая кристаллизация этого компонента возможна лишь при понижении температуры. Таким образом, кристаллизация одного компонента из раствора происходит не при одной температуре, как в случае чистого вещества, а в некотором интервале температур. Поскольку кристаллизация вещества происходит небольшими порциями, то выделяющейся теплоты кристаллизации недостаточно для температурной остановки: происходит лишь уменьшение скорости охлаждения, кривая охлаждения становится более пологой.
По мере выделения одного из компонентов в третью фазу, происходит накапливание второго компонента в растворе. Наконец при некоторой температуре раствор становится насыщенным по отношению и ко второму компоненту, т.е. начинается кристаллизация обоих компонентов одновременно.
Смесь кристаллов, образующихся при совместной кристаллизации двух компонентов, называется эвтектикой.
Эвтектика имеет определенный состав, наименьшую и всегда постоянную (эвтектическую) температуру кристаллизации (плавления) при данном давлении. Если взять расплав, соответствующий составу эвтектики, то кривая охлаждения будет иметь вид (рисунок 2.5 в). В сплавах, отличающихся по составу от эвтектического, всегда первым будет кристаллизоваться компонент, находящийся в избытке по сравнению с составом эвтектики, а затем, когда избыток выкристаллизуется, а состав станет равным эвтектическому, будет кристаллизоваться эвтектика. Таким образом, у сплавов с различным составом начинается кристаллизация при различных температурах, а заканчивается при одной и той же, эвтектической температуре. Анализируя кривые охлаждения, находят температуры начала кристаллизации расплавов и, нанеся эти точки на диаграмму Т – состав получают линию ликвидуса, а соединяя точки, отвечающие температуре конца затвердевания, вычерчивают линию солидуса. Так получают диаграмму плавкости.

Рисунок 2.5 – Типы кривых охлаждения:
а – для чистого вещества А;
б – для смеси веществ А + В;
в – для эвтектической смеси;
г – кривая охлаждения в случае оразования метастабильного состояния (переохлажденного состояния);
д – для системы, где нет фазовых превращений
Дата добавления: 2016-06-22; просмотров: 2779;











